题目内容
2.化简或解方程组(1)($\sqrt{6}$-2$\sqrt{15}$)×$\sqrt{3}$
(2)$\frac{\sqrt{20}+\sqrt{5}}{\sqrt{45}}$-$\sqrt{\frac{1}{3}}$×$\sqrt{6}$
(3)$\left\{\begin{array}{l}{4m+3n=5}\\{2m-n=5}\end{array}\right.$
(4)$\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=6}\\{4x-3y=8}\end{array}\right.$.
分析 (1)根据乘法分配律去括号,再化简各二次根式即可得;
(2)先化简各二次根式,再计算乘、除运算可得;
(3)加减消元法求解即可;
(4)加减消元法求解即可.
解答 解:(1)原式=$\sqrt{18}$-2$\sqrt{45}$=3$\sqrt{2}$-6$\sqrt{5}$;
(2)原式=$\frac{2\sqrt{5}+\sqrt{5}}{3\sqrt{5}}$-$\sqrt{2}$=1-$\sqrt{2}$;
(3)解方程组$\left\{\begin{array}{l}{4m+3n=5}&{①}\\{2m-n=5}&{②}\end{array}\right.$,
②×3+①,得:10m=20,m=2,
将m=2代入②,得:4-n=5,n=-1,
故方程组的解为:$\left\{\begin{array}{l}{m=2}\\{n=-1}\end{array}\right.$;
(4)解方程组$\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=6}&{①}\\{4x-3y=8}&{②}\end{array}\right.$,
①×12+②,得:8x=80,x=10,
将x=10代入②,得:40-3y=8,解得:y=$\frac{32}{3}$,
故方程组的解为:$\left\{\begin{array}{l}{x=10}\\{y=\frac{32}{3}}\end{array}\right.$.
点评 本题主要考查二次根式的混合运算及解方程组的能力,熟练掌握二次根式的混合运算顺序和二次根式的性质是解题的关键.

练习册系列答案
相关题目
12.算式-80的值是( )
| A. | $-\frac{1}{8}$ | B. | 1 | C. | -1 | D. | $\frac{1}{8}$ |
10.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要( )个小立方块.
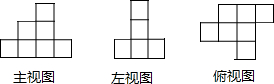

| A. | 36 | B. | 52 | C. | 54 | D. | 55 |
17.小颖对青岛地区6、7月份天气连续十天每天的最高气温进行统计,依次得到以下一组数据:24,25,26,24,26,27,27,26,27,27(单位℃).则这组数据的中位数和众数分别是( )
| A. | 27,26 | B. | 27,26.5 | C. | 26.5,27 | D. | 26,27 |
11.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. | 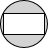 | D. | 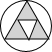 |
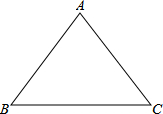 已知△ABC中,AB=AC=5,BC=6(如图所示),将△ABC沿射线BC方向平移m个单位得到△DEF,顶点A、B、C分别与D、E、F对应.若以点A、D、E为顶点的三角形是等腰三角形,且AE为腰,则m的值是6或$\frac{25}{6}$.
已知△ABC中,AB=AC=5,BC=6(如图所示),将△ABC沿射线BC方向平移m个单位得到△DEF,顶点A、B、C分别与D、E、F对应.若以点A、D、E为顶点的三角形是等腰三角形,且AE为腰,则m的值是6或$\frac{25}{6}$.
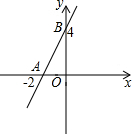 如图,直线y=kx+b交坐标轴于A,B两点,则不等式kx+b≤0的解集在数轴上表示正确的是( )
如图,直线y=kx+b交坐标轴于A,B两点,则不等式kx+b≤0的解集在数轴上表示正确的是( )