题目内容
6.用配方法确定抛物线y=-$\frac{1}{3}{x}^{2}$-x+$\frac{1}{4}$的顶点坐标、对称轴.分析 化为一般式后,利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
解答 解:y=-$\frac{1}{3}$x2-x+$\frac{1}{4}$
=-$\frac{1}{3}$(x2+3x)+$\frac{1}{4}$
=-$\frac{1}{3}$(x2+3x+$\frac{9}{4}$-$\frac{9}{4}$)+$\frac{1}{4}$
=-$\frac{1}{3}$(x+$\frac{3}{2}$)2+$\frac{3}{4}$+$\frac{1}{4}$
=-$\frac{1}{3}$(x+$\frac{3}{2}$)2+1
∴抛物线y=-$\frac{1}{3}$x2-x+$\frac{1}{4}$的顶点坐标是(-$\frac{3}{2}$,1),对称轴是x=-$\frac{3}{2}$.
点评 本题考查了二次函数的解析式有三种形式:
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;
(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
相关题目
1. 如图,在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是( )
如图,在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是( )
 如图,在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是( )
如图,在△ABC中,AB=5,AC=3,则BC边上的中线AD的取值范围是( )| A. | 2<AD<8 | B. | 0<AD<8 | C. | 1<AD<4 | D. | 3<AD<5 |
18. 如图,当y>0时,自变量x的范围是( )
如图,当y>0时,自变量x的范围是( )
 如图,当y>0时,自变量x的范围是( )
如图,当y>0时,自变量x的范围是( )| A. | x<1 | B. | x≤0 | C. | x>1 | D. | x≥0 |
16.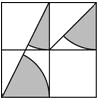 如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
 如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )| A. | $\frac{1}{4}$π | B. | $\frac{3}{4}$π | C. | $\frac{5}{8}$π | D. | $\frac{3}{8}$π |
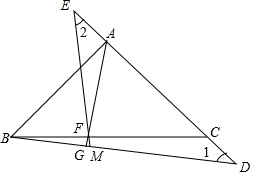 等腰Rt△ABC中,AC=AB,∠BAC=90°,点D、E是AC上两点且AD=CE,AF⊥BD于点G,交BC于点F,连接EF交BD于点M,求证:∠1=∠2.
等腰Rt△ABC中,AC=AB,∠BAC=90°,点D、E是AC上两点且AD=CE,AF⊥BD于点G,交BC于点F,连接EF交BD于点M,求证:∠1=∠2.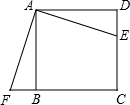 如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.