题目内容
17.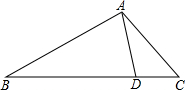 如图,D是△ABC的边BC上一点,已知AB=2,AD=1,∠DAC=∠B,则$\frac{CD}{BD}$=$\frac{1}{3}$.
如图,D是△ABC的边BC上一点,已知AB=2,AD=1,∠DAC=∠B,则$\frac{CD}{BD}$=$\frac{1}{3}$.
分析 根据相似三角形的判定得出△DAC∽△ABC,根据相似三角形的性质得出$\frac{AC}{BC}$=$\frac{CD}{AC}$=$\frac{AD}{AB}$,根据AB=2,AD=1求出BC=2AC,AC=2CD,求出BD=3CD,即可得出答案.
解答 解:∵∠DAC=∠B,∠C=∠C,
∴△DAC∽△ABC,
∴$\frac{AC}{BC}$=$\frac{CD}{AC}$=$\frac{AD}{AB}$,
∵AB=2,AD=1,
∴BC=2AC,AC=2CD,
∴BC=4CD,
∴BD=3CD,
∴$\frac{CD}{BD}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了相似三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
12.平面直角坐标系中有一点P,点P到y轴的距离为2,点P的纵坐标为-3,则点P的坐标是( )
| A. | (-3,-2) | B. | (-2,-3) | C. | (2,-3) | D. | (2,-3)或(-2,-3) |
7. 小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
 小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )
小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )| A. | 小亮在图书馆停留的时间是15分钟 | |
| B. | 小亮从学校去图书馆的速度和从图书馆返回学校的速度相同 | |
| C. | 小明离开学校的路程s(千米)与时间t(分)之间的函数关系式为S=$\frac{4}{45}$t | |
| D. | BC段s(千米)与t(分)之间的函数关系式为S=$\frac{4}{45}$t+12 |
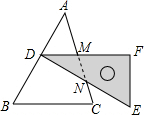 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,且DE⊥AB,∠A=50°,BC∥DF,则∠DNM的度数为40°.
如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,且DE⊥AB,∠A=50°,BC∥DF,则∠DNM的度数为40°.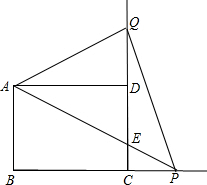 如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t.
如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t. 如图,直线a∥b,∠1=60°,∠2=50°,则∠3=70°.
如图,直线a∥b,∠1=60°,∠2=50°,则∠3=70°.