题目内容
9．等腰三角形一边长为4，一边长等于9，则它的周长等于（ ）| A． | 17 | B． | 22 | C． | 13 | D． | 17或22 |
分析 题目给出等腰三角形有两条边长为4和9，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．
解答 解：分两种情况：
当腰为4时，4+4＜9，所以不能构成三角形；
当腰为9时，9+9＞4，9-9＜4，所以能构成三角形，周长是：9+9+4=22．
故选B．
点评 本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
练习册系列答案
相关题目
20．在-6，9.3，-2π，3.3030030003…，$\frac{22}{7}$这5个数中，无理数有（ ）
| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
17．若a＞1，则a，-a，$\frac{1}{a}$从大到小排列正确的是（ ）
| A． | a＞-a＞$\frac{1}{a}$ | B． | a＞$\frac{1}{a}$＞-a | C． | $\frac{1}{a}$＞-a＞a | D． | $\frac{1}{a}$＞-a＞a＞ |
4．下列图形中，绕着某点旋转90°后可以与原来图形重合的是（ ）
| A． |  | B． |  | C． |  | D． |  |
14．
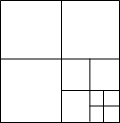如图，连接边长为1的正方形对边中点，可将一个正方形分成4个大小相同的小正方形，选右下角的小正方形进行第二次操作，又可将这个小正方形分成4个更小的小正方形…重复这样的操作，则5次操作后右下角的小正方形面积是（ ）
如图，连接边长为1的正方形对边中点，可将一个正方形分成4个大小相同的小正方形，选右下角的小正方形进行第二次操作，又可将这个小正方形分成4个更小的小正方形…重复这样的操作，则5次操作后右下角的小正方形面积是（ ）| A． | （$\frac{1}{4}$）5 | B． | （$\frac{1}{2}$）5 | C． | $\frac{1}{5}$ | D． | 1-（$\frac{1}{4}$）5 |
1．（-$\sqrt{3}$）2等于（ ）
| A． | -3 | B． | 3 | C． | -$\frac{1}{3}$ | D． | $\frac{1}{3}$ |
18．已知A（m，y1）和B（-2，y2）是函数y=-$\frac{6}{x}$上的点，且y1＞y2，则m的取值范围是（ ）
| A． | -2＜m＜0 | B． | m＞-2 | C． | m＜-2 | D． | m＜-2或m＞0 |
19．
如图，在Rt△ABC中，∠C=90°，AC=4，AB=5，则cosA的值是（ ）
如图，在Rt△ABC中，∠C=90°，AC=4，AB=5，则cosA的值是（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |