题目内容
4.计算:(1)(-x)•x2•(-x)6;
(2)y•ym-1-3y3•ym-3;
(3)(-2a)3-(-a)•(3a)2;
(4)(y4)2÷(y2)3•y2;
(5)(x-y)3•(x-y)2•(y-x);
(6)(22010-22009)0-(-$\frac{1}{4}$)-2+(-0.125)2009×82010;
(7)(3x2y-2x+1)(-2xy);
(8)(4×106)×(-$\frac{1}{2}$×10-3);
(9)(-4am+1)3÷[2(2am)2•a];
(10)5ab3•(-$\frac{3}{4}$a3b2)•(-$\frac{2}{3}$ab4c)3.
分析 (1)先整理符号,再根据同底数幂运算可得;
(2)先计算同底数幂相乘,再合并;
(3)先计算积的乘方,再计算同底数幂相乘,最后合并可得;
(4)先计算幂的乘方,再计算同底数幂的除法和乘法可得;
(5)先将底数统一,再根据同底数幂运算法则可得;
(6)根据实数的混合运算及逆用积的乘方可得;
(7)根据多项式乘单项式的法则可得;
(8)利用同底数幂的运算法则计算可得;
(9)先计算积的乘方、再计算幂的乘方,最后计算单项式的除法;
(10)先计算单项式的乘方,再计算乘法可得.
解答 解:(1)原式=-x•x2•x6=-x9;
(2)原式=ym-3ym=-2ym;
(3)原式=-8a3+a•9a2=-8a3+9a3=a3;
(4)原式=y8÷y6•y2=y2•y2=y4;
(5)原式=-(x-y)3•(x-y)2•(x-y)=-(x-y)6;
(6)原式=1-16-($\frac{1}{8}$)2009×82009×8
=-15-($\frac{1}{8}$×8)2009×8
=-15-8
=-23;
(7)原式=-6x3y2+4x2y-2xy;
(8)原式=(-$\frac{1}{2}$×4)×(106×10-3)=-2×103;
(9)原式=-64a3m+3÷(8a2m+1)=-8am+2;
(10)原式=-$\frac{15}{4}$a4b5•(-$\frac{8}{27}$a3b12c3)=$\frac{10}{9}$a7b17c3.
点评 本题主要考查幂的运算及整式的混合运算,熟练掌握幂的运算法则和整式的混合运算顺序、法则是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.在下列平面汽车图标中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.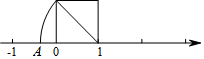 如图,以数轴的单位长度线段为边作一个正方形,以原点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以原点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
 如图,以数轴的单位长度线段为边作一个正方形,以原点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以原点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )| A. | 1 | B. | -1 | C. | 1-$\sqrt{2}$ | D. | $\sqrt{2}$ |
14.已知,在四边形ABCD中,∠A=∠B=90°,要使四边形ABCD为矩形,那么需要添加的一个条件是( )
| A. | AB=BC | B. | AD=BC | C. | AD=AB | D. | BC=CD |
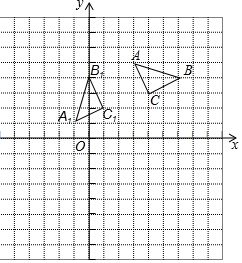 如图,平面直角坐标系建立在边长为1个单位长度的小正方形组成的网格中,格点△ABC的顶点在网格线的交点上,将△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
如图,平面直角坐标系建立在边长为1个单位长度的小正方形组成的网格中,格点△ABC的顶点在网格线的交点上,将△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.