题目内容
16.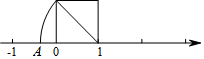 如图,以数轴的单位长度线段为边作一个正方形,以原点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以原点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )| A. | 1 | B. | -1 | C. | 1-$\sqrt{2}$ | D. | $\sqrt{2}$ |
分析 先根据勾股定理求出AC的长,再根据数轴上两点间的距离公式求出点A表示的数即可.
解答  解:∵正方形的边长为1,
解:∵正方形的边长为1,
∴BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴AC=$\sqrt{2}$,即|A-1|=$\sqrt{2}$,
故点A表示1-$\sqrt{2}$.
故选:C.
点评 本题考查了实数与数轴的对应关系,以及勾股定理和正方形的性质,熟知数轴上各点与实数是一一对应关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.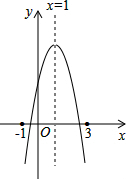 如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为( )
如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为( )
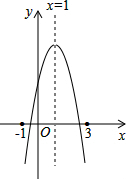 如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为( )
如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.若x>y,则下列式子错误的是( )
| A. | x+2>y+2 | B. | -2x<-2y | C. | 1-x>1-y | D. | $\frac{x}{2}>\frac{y}{2}$ |
 如图,一个用篱笆围成的长方形的面积是500m2.
如图,一个用篱笆围成的长方形的面积是500m2.
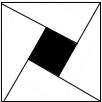 如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,那么tanβ=$\frac{4}{3}$.
如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,那么tanβ=$\frac{4}{3}$.