题目内容
14.某村为了确保村民生活生产用水,春季准备由村委会和村民共同集资新建储水池和维护原有储水池共20个.费用和可供使用的户数及占地情况如下表:| 储水池 | 费用(万元/个) | 可供使用户数(户/个) | 占地面积(m2/个) |
| 新建 | 4 | 5 | 4 |
| 维护 | 3 | 18 | 6 |
请解答下列问题:
(1)有几种实施方案?
(2)若每户村民平均集资0.2万元,村委会最少出资多少钱?
(3)在(2)的条件下,由甲、乙两个施工队共同承包此项工程,已知甲施工队新建一个储水池和维护两个储水池,恰好用7天;乙施工队新建一个储水池和维护4个储水池恰好用12天.直接写出甲、乙两队各施工多少天?(两施工队的工作天数都是整数)
分析 (1)根据图表,列出不等式组,确定实施方案;
(2)根据实施方案,确定所需的费用,使总费用最小,然后求出村民筹集的资金加上村委会的出资款和所需的总费用进行比较即可;
(3)设甲队干了x天,乙队干了y天,列出方程组解答即可.
解答 (1)解:设新建a个,维护6个,根据题意可得:$\left\{\begin{array}{l}{a+b=20}\\{4a+6b≤109}\\{5a+18b≥243}\end{array}\right.$,
解不等式组得:$\left\{\begin{array}{l}{b≤14.5}\\{b≥11}\end{array}\right.$,
∴b可取11,12,13,14,则a可取9,8,7,6;
∴有4种方案①$\left\{\begin{array}{l}{a=9}\\{b=11}\end{array}\right.$; ②$\left\{\begin{array}{l}{a=8}\\{b=12}\end{array}\right.$;③$\left\{\begin{array}{l}{a=7}\\{b=13}\end{array}\right.$; ④$\left\{\begin{array}{l}{a=6}\\{b=14}\end{array}\right.$;
(2)∵M=4a+3b=-b+80,M随b的增大而减小,
∴只有b取最大值时,M有最小值.
即最小出资为:-14+80=66;
村民出资为a2×243=48.6,村委会出资为:66-48.6=17.4,
∴村委会最少出资17.4万元.
(3)设甲队干了x天,乙队干了y天,由题意可得:$\left\{\begin{array}{l}{\frac{x}{7}+\frac{y}{12}=6}\\{\frac{2x}{7}+\frac{4y}{12}=14}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=35}\\{y=12}\end{array}\right.$,
答:甲干了35天;乙干了12天.
点评 本题考查不等式的综合应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量之间的等量(或不等)关系,准确的列出式子.

 名校课堂系列答案
名校课堂系列答案| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不确定 |
| A. | 6个只有颜色不同的小球 | |
| B. | 两个骰子 | |
| C. | 三个硬币 | |
| D. | 只有颜色不同的小卡片6张,其中红、白、黄各占2张 |
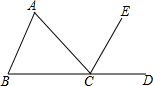 如图,点B、C、D在同一直线上,∠A=∠B.
如图,点B、C、D在同一直线上,∠A=∠B.