题目内容
9.(1)-22+(π-$\sqrt{3}$)0+($\frac{1}{3}$)-2+$\sqrt{27}$-9tan30°(2)先化简,自求值.
(1-$\frac{2}{a}$)+$\frac{{a}^{2}-4a+4}{{a}^{2}-4}$-$\frac{a+4}{a+2}$,其中a2+2a-15=0.
分析 (1)根据二次根式化简,绝对值的定义、负整数指数幂和零指数幂的性质进行计算,然后根据实数的运算法则求得计算结果;
(2)根据分式的四则混合运算进行计算即可.
解答 解:(1)-22+(π-$\sqrt{3}$)°+($\frac{1}{3}$)-2+$\sqrt{27}$-9tan30°
=-4+1+9+3$\sqrt{3}$-9×$\frac{\sqrt{3}}{3}$
=-4+1+9+3$\sqrt{3}$-3$\sqrt{3}$
=6;
(2)原式=$\frac{a-2}{a}$•$\frac{(a-2)(a+2)}{(a-2)^2}$-$\frac{a+4}{a+2}$
=$\frac{a+2}{a}$-$\frac{a+4}{a+2}$
=$\frac{(a+2)^2-a(a+4)}{a(a+2)}$
=$\frac{a^2+4a+4-a^2-4a}{a(a+2)}$
=$\frac{4}{a(a+2)}$
=$\frac{4}{a^2+2a}$,
∵a2+2a-15=0
∴a2+2a=15,
∴原式=$\frac{4}{15}$.
点评 本题考查了二次根式化简,绝对值的定义、负整数指数幂和零指数幂的性质,分式的四则混合运算,熟练掌握运算法则是解题的关键.

练习册系列答案
相关题目
19.十一黄金周时期,某旅游区的游客知表:
(1)求这7天假期中,游客量的平均数、中位数和众数;
(2)选用平均数、中位数和众数中的哪个数作代表,更能反映黄金周7天游客量的一般情况?
| 人数/万人 | 0.6 | 1.2 | 2 | 2.5 |
| 天数 | 2 | 1 | 3 | 1 |
(2)选用平均数、中位数和众数中的哪个数作代表,更能反映黄金周7天游客量的一般情况?
20.四个数-5,0,1,2$\sqrt{3}$,其中负数是( )
| A. | -5 | B. | 0 | C. | 1 | D. | 2$\sqrt{3}$ |
 如图,将放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
如图,将放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.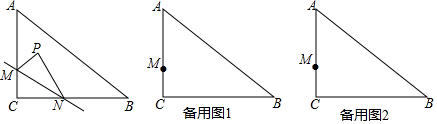
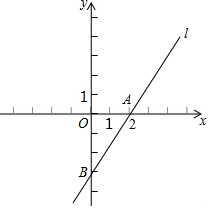 如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx-3与y轴交于点B.
如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx-3与y轴交于点B.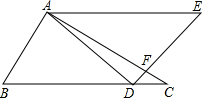 将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.
将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.