题目内容
14.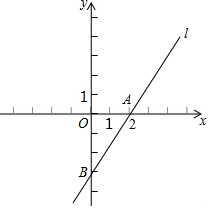 如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx-3与y轴交于点B.
如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx-3与y轴交于点B.(1)求直线l的表达式;
(2)若点C是直线l与双曲线y=$\frac{n}{x}$的一个公共点,AB=2AC,直接写出n的值.
分析 (1)将点A坐标代入直线解析式求得m即可;
(2)先求出点B坐标,再分点C在BA延长线上和点C在线段AB上两种情况,利用相似三角形的判定与性质求出点C的坐标即可.
解答 解:(1)∵直线l:y=mx-3过点A(2,0),
∴0=2m-3.
∴$m=\frac{3}{2}$.
∴直线l的表达式为$y=\frac{3}{2}x-3$;
(2)当x=0时,y=-3,
∴点B(0,-3),
如图1,当点C在BA延长线上时,作CD⊥y轴于点D,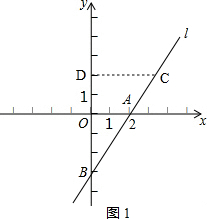
则△BAO∽△BCD,
∴$\frac{BA}{BC}$=$\frac{BO}{BD}$=$\frac{OA}{CD}$,即$\frac{2}{3}$=$\frac{3}{3+OD}$=$\frac{2}{CD}$,
解得:CD=3,OD=$\frac{3}{2}$,
∴点C(3,$\frac{3}{2}$),
则n=3×$\frac{3}{2}$=$\frac{9}{2}$;
如图2,当点C在线段AB上时,作CE⊥y轴于点E,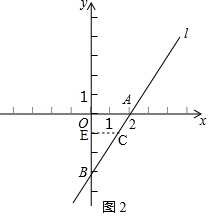
则△BAO∽△BCE,
∴$\frac{BC}{BA}$=$\frac{CE}{AO}$=$\frac{BE}{BO}$,即$\frac{1}{2}$=$\frac{CE}{2}$=$\frac{BE}{3}$,
解得:CE=1,BE=3,
∴OE=BO-BE=$\frac{3}{2}$,
∴点C的坐标为(1,-$\frac{3}{2}$),
则n=-$\frac{3}{2}$,
综上,n=$-\frac{3}{2}$或$\frac{9}{2}$.
点评 本题主要考查直线和双曲线的交点问题,熟练掌握待定系数法求函数解析式和相似三角形的判定与性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
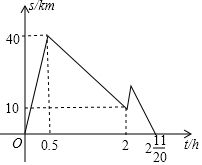 甲、乙两辆汽车同时从A地出发前往相距250千米的B地,乙车先出发匀速行驶,一段时间后,甲车出发匀速追赶,途中因油料不足,甲到服务区加油花了6分钟,为了尽快追上乙车,甲车提高速度仍保持匀速行驶,追上乙车后继续保持这一速度直到B地,如图是甲、乙两车之间的距离s(km2),乙车出发时间t(h)之间的函数关系图象,则甲车比乙车早到11.5分钟.
甲、乙两辆汽车同时从A地出发前往相距250千米的B地,乙车先出发匀速行驶,一段时间后,甲车出发匀速追赶,途中因油料不足,甲到服务区加油花了6分钟,为了尽快追上乙车,甲车提高速度仍保持匀速行驶,追上乙车后继续保持这一速度直到B地,如图是甲、乙两车之间的距离s(km2),乙车出发时间t(h)之间的函数关系图象,则甲车比乙车早到11.5分钟. 如图所示的几何体是由四个完全相同的正方体组成的,这个几何体的俯视图是( )
如图所示的几何体是由四个完全相同的正方体组成的,这个几何体的俯视图是( )



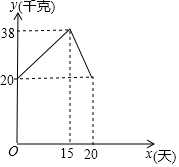 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装江米20千克,为迎接今年5月30日的“端午节”,该超市决定在节前20天增加每天包装江米的质量,包装质量与天数的变化情况如图所示,节日后又恢复到原来每天包装的质量.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装江米20千克,为迎接今年5月30日的“端午节”,该超市决定在节前20天增加每天包装江米的质量,包装质量与天数的变化情况如图所示,节日后又恢复到原来每天包装的质量.