题目内容
1.有五张正面分别标有数字0,1,2,3,4的不透明卡片,它们除数字不同外,其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为n,则使关于x的分式方程$\frac{1-nx}{x-2}+2=\frac{1}{2-x}$有解的概率为$\frac{3}{5}$.分析 去分母化分式方程为整式方程,求出x=$\frac{2}{2-n}$,根据方程有解得出满足条件的n的值,根据概率公式可得答案.
解答 解:∵1-nx+2x-4=-1,
∴(2-n)x=2,
则x=$\frac{2}{2-n}$,
由分式方程有解可得n≠2且n≠1,
∴使关于x的分式方程$\frac{1-nx}{x-2}+2=\frac{1}{2-x}$有解的概率为$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 此题考查了概率公式的应用及分式方程.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列式子为最简二次根式的是( )
| A. | $\sqrt{7}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{\frac{1}{2}}$ |
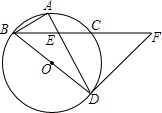 如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4.
如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4. 如图,在?ABCD中,E,F,G,H各点分别在AB,BC,CD,DA上,且AE=BF=CG=DH.求证:EG与FH互相平分.
如图,在?ABCD中,E,F,G,H各点分别在AB,BC,CD,DA上,且AE=BF=CG=DH.求证:EG与FH互相平分.