题目内容
若关于x的方程(k+1)x2-(k-2)x-5+k=0只有唯一的一个解,则k= ,此方程的解为 .
考点:根的判别式,一元一次方程的解
专题:
分析:因为方程只有一个实数根,则方程为一元一次方程,据此可以得到k的值.
解答:解:∵方程只有一个实数根,
∴k+1=0,k-2≠0
解得:k=-1;
此时方程为3x-6=0,
解得x=2.
故答案为:-1,2.
∴k+1=0,k-2≠0
解得:k=-1;
此时方程为3x-6=0,
解得x=2.
故答案为:-1,2.
点评:此题考查一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.

练习册系列答案
相关题目
 如图,点A、B、C三点均在⊙O上,∠B=∠C.以下结论错误的是( )
如图,点A、B、C三点均在⊙O上,∠B=∠C.以下结论错误的是( )| A、AB=AC | ||||
B、
| ||||
C、
| ||||
| D、∠BOC=80° |
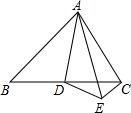 如图,在△ABC中,D是BC的中点,DE⊥AD,∠EAD=∠BAD.
如图,在△ABC中,D是BC的中点,DE⊥AD,∠EAD=∠BAD.