题目内容
 已知四边形ABCD顶点都在4×4的正方形网格格点上,如图所示,
已知四边形ABCD顶点都在4×4的正方形网格格点上,如图所示,(1)请画出四边形ABCD的外接圆,并标明圆心M的位置;
(2)这个圆中弦BC所对的圆周角的度数是
考点:圆内接四边形的性质,圆心角、弧、弦的关系,圆周角定理
专题:
分析:(1)由垂径定理可知弦的垂直平分线过圆心,所以可作AB、AD的垂直平分线,其交点即为圆心M;
(2)连接BM,MC,可求得BM=CM=
,BC=
,所以可得△BMC为等腰直角三角形,所以∠BMC=90°,故可知弦BC所对的圆周角为45°.
(2)连接BM,MC,可求得BM=CM=
| 5 |
| 10 |
解答:
解:
(1)如图1,分别作AB、AC的垂直平分线,交于点M,由垂径定理可知点M即为四边形ABCD外接圆的圆心;
(2)如图2,连接BM,MC,则可求得MB=MC=BM=CM=
,BC=
,
所以△BMC为等腰直角三角形,
所以∠BMC=90°,
故可知弦BC所对的圆周角为45°.
故答案为:45°.

解:
(1)如图1,分别作AB、AC的垂直平分线,交于点M,由垂径定理可知点M即为四边形ABCD外接圆的圆心;
(2)如图2,连接BM,MC,则可求得MB=MC=BM=CM=
| 5 |
| 10 |
所以△BMC为等腰直角三角形,
所以∠BMC=90°,
故可知弦BC所对的圆周角为45°.
故答案为:45°.
点评:本题主要考查垂径定理及圆周角定理,利用垂径定理找到圆心M是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
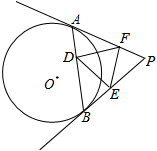 如图,PA、PB切⊙O于点A、B,连结AB,在AB、PA、PB上分别取点D、F、E,使AD=BE,BD=AF,连结DE、DF、EF,若∠P=α,求∠EDF(用含α的代数式表示)
如图,PA、PB切⊙O于点A、B,连结AB,在AB、PA、PB上分别取点D、F、E,使AD=BE,BD=AF,连结DE、DF、EF,若∠P=α,求∠EDF(用含α的代数式表示) 如图,已知AO⊥OB于O,∠2-∠1=20°,求∠1,∠2的度数.
如图,已知AO⊥OB于O,∠2-∠1=20°,求∠1,∠2的度数.