题目内容
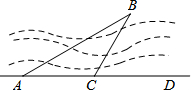如图，小明要测量河内小岛B到河边公路AD的距离，在A点测得∠BAD=30°，在C点测得∠BCD=60°，又测得AC=50米，求小岛B到公路AD的距离．考点：解直角三角形的应用
专题：
分析：利用三角形外角的性质得出∠ABC=30°，进而得出BC=AC的长，再利用锐角三角函数关系得出BE的长，即可得出答案．
解答：
解：过B作BE⊥AD于E
∵∠BAD=30°，∠BCE=60°，
∴∠ABC=30°．
∴∠ABC=∠BAD=30°．
∴BC=AC=50（米）．
在Rt△BCE中，sin∠BCD=
=
．
解得：BE=25
（米）．
答：小岛B到公路AD的距离是25
米．
解：过B作BE⊥AD于E∵∠BAD=30°，∠BCE=60°，
∴∠ABC=30°．
∴∠ABC=∠BAD=30°．
∴BC=AC=50（米）．
在Rt△BCE中，sin∠BCD=
| BD |
| BC |
| ||
| 2 |
解得：BE=25
| 3 |
答：小岛B到公路AD的距离是25
| 3 |
点评：此题主要考查了解直角三角形的应用，根据题意得出BC=AC是解题关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
某道路一侧原有路灯106盏，相邻两盏灯的距离为36米，现计划全部更换为新型的节能灯，且相邻两盏灯的距离变为70米．设需更换的新型节能灯为x盏，则可列方程（ ）
| A、70x=106×36 |
| B、70×（x+1）=36×（106+1） |
| C、106-x=70-36 |
| D、70（x-1）=36×（106-1） |
已知a3＜0，b2≥0，那么关于ab的值下列说法正确的是（ ）
| A、ab＞0 | B、ab＜0 |
| C、ab=0 | D、以上都可能 |
如图所示，∠AOB=α，∠AOB内有一点P，在∠AOB的两边上有两个动点Q、R（均不同于点O），现在把△PQR周长最小时∠QPR的度数记为β，则α与β应该满足关系是