题目内容
某道路一侧原有路灯106盏,相邻两盏灯的距离为36米,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70米.设需更换的新型节能灯为x盏,则可列方程( )
| A、70x=106×36 |
| B、70×(x+1)=36×(106+1) |
| C、106-x=70-36 |
| D、70(x-1)=36×(106-1) |
考点:由实际问题抽象出一元一次方程
专题:
分析:设需更换的新型节能灯为x盏,根据等量关系:两种安装路灯方式的道路总长相等,列出方程即可.
解答:解:设需更换的新型节能灯为x盏,根据题意得
70(x-1)=36×(106-1).
故选D.
70(x-1)=36×(106-1).
故选D.
点评:本题考查了由实际问题抽象出一元一次方程,关键是找出题目中的相等关系.

练习册系列答案
相关题目
若方程2x3-5m+5(m-1)=0是关于x的一元一次方程,则这个方程的解是( )
A、
| ||
B、-
| ||
C、
| ||
| D、3 |
直线y=kx+3经过点(1,4),则k的值是( )
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
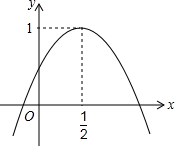 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
一个矩形的长比宽相多3cm,面积是25cm2,求这个矩形的长和宽.设矩形的宽为xcm,则所列方程正确的是( )
| A、x2-3x+25=0 |
| B、x2-3x-25=0 |
| C、x2+3x-25=0 |
| D、x2+3x-50=0 |
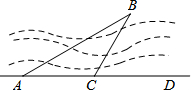 如图,小明要测量河内小岛B到河边公路AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,求小岛B到公路AD的距离.
如图,小明要测量河内小岛B到河边公路AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,求小岛B到公路AD的距离.