题目内容
8.甲、乙两人进行射击比赛,他们5次射击的成绩(单位:环)如图所示:设甲、乙两人射击成绩的平均数依次为$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,射击成绩的方差依次为$S_甲^2$、$S_乙^2$,那么下列判断中正确的是( )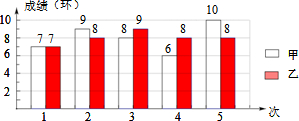
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2=S_乙^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2>S_乙^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ |
分析 根据平均数和方差的计算公式分别进行计算,再进行比较,即可得出答案.
解答 解:∵$\overline{{x}_{甲}}$=(7+9+8+6+10)÷5=8,$\overline{{x}_{乙}}$,=(7+8+9+8+8)÷5=8,
∴$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,
∵$S_甲^2$=$\frac{1}{5}$[(7-8)2+(9-8)2+(8-8)2+(6-8)2+(10-8)2]=2,
$S_乙^2$=$\frac{1}{5}$[(7-8)2+(8-8)2+(9-8)2+(8-8)2+(8-8)2]=0.4,
∴$S_甲^2$>$S_乙^2$;
故选B.
点评 此题考查了平均数和方差,掌握平均数和方差公式是解题的关键,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
19.据统计,中国每年浪费的食物总量折合粮食约为50000000吨,将50000000用科学记数法表示为( )
| A. | 5×107 | B. | 50×106 | C. | 5×106 | D. | 0.5×108 |
13.为了倡导绿色出行,某市为市民提供了自行车租赁服务,其收费标准如下:
如果小明某次租赁自行车3小时,缴费14元,请判断小明该次租赁自行车所在地区的类别是B类(填“A、B、C”中的一个).
| 地区类别 | 首小时内 | 首小时外 | 备注 |
| A类 | 1.5元/15分钟 | 2.75元/15分钟 | 不足15分钟时 按15分钟收费 |
| B类 | 1.0元/15分钟 | 1.25元/15分钟 | |
| C类 | 免费 | 0.75元/15分钟 |
20. 如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
 如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
17.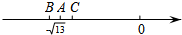 如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
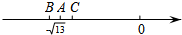 如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )| A. | 4和5 | B. | -5和-4 | C. | 3和4 | D. | -4和-3 |
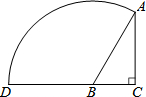 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,则$\widehat{AD}$的长为$\frac{4π}{3}$.
如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,则$\widehat{AD}$的长为$\frac{4π}{3}$.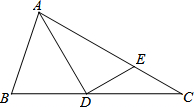 已知,△ABC中,D是BC上的一点,且∠DAC=30°,过点D作ED⊥AD交AC于点E,AE=4,EC=2.
已知,△ABC中,D是BC上的一点,且∠DAC=30°,过点D作ED⊥AD交AC于点E,AE=4,EC=2. 如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.
如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.