题目内容
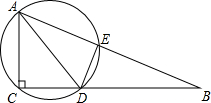 如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.(1)求证:AC=AE;
(2)求△ACD外接圆的直径.
考点:三角形的外接圆与外心,全等三角形的判定与性质,勾股定理
专题:
分析:(1)先根据:∠ACB=90°得出AD为⊙O的直径故可得出∠ACB=∠AED.再由AD是△ABC中∠BAC的平分线可知∠CAD=∠EAD,由HL定理得出△ACD≌△AED,根据全等三角形的性质可知AC=AE;
(2)先根据勾股定理求出AB的长,设CD=DE=x,则DB=BC-CD=8-x,EB=AB-AE=10-6=4,在Rt△BED中,根据勾股定理得出x的值,再由△ACD是直角三角形即可得出AD的长.
(2)先根据勾股定理求出AB的长,设CD=DE=x,则DB=BC-CD=8-x,EB=AB-AE=10-6=4,在Rt△BED中,根据勾股定理得出x的值,再由△ACD是直角三角形即可得出AD的长.
解答: (1)证明:∵∠ACB=90°,且∠ACB为⊙O的圆周角,
(1)证明:∵∠ACB=90°,且∠ACB为⊙O的圆周角,
∴AD为⊙O的直径,
∴∠AED=90°,
∴∠ACB=∠AED.
∵AD是△ABC中∠BAC的平分线,
∴∠CAD=∠EAD,
∴CD=DE,
在Rt△ACD与Rt△AED中,
,
∴△ACD≌△AED(HL),
∴AC=AE;
(2)∵△ABC是直角三角形,且AC=6,BC=8,
∴AB=
=
=10,
∵由(1)得,∠AED=90°,
∴∠BED=90°.
设CD=DE=x,则DB=BC-CD=8-x,EB=AB-AE=10-6=4,
在Rt△BED中,根据勾股定理得,BE2=BE2+ED2,即(8-x)2=x2+42,解得x=3,
∴CD=3,
∵AC=6,△ACD是直角三角形,
∴AD2=AC2+CD2=62+32=45,
∴AD=3
.
 (1)证明:∵∠ACB=90°,且∠ACB为⊙O的圆周角,
(1)证明:∵∠ACB=90°,且∠ACB为⊙O的圆周角,∴AD为⊙O的直径,
∴∠AED=90°,
∴∠ACB=∠AED.
∵AD是△ABC中∠BAC的平分线,
∴∠CAD=∠EAD,
∴CD=DE,
在Rt△ACD与Rt△AED中,
|
∴△ACD≌△AED(HL),
∴AC=AE;
(2)∵△ABC是直角三角形,且AC=6,BC=8,
∴AB=
| AC2+BC2 |
| 62+82 |
∵由(1)得,∠AED=90°,
∴∠BED=90°.
设CD=DE=x,则DB=BC-CD=8-x,EB=AB-AE=10-6=4,
在Rt△BED中,根据勾股定理得,BE2=BE2+ED2,即(8-x)2=x2+42,解得x=3,
∴CD=3,
∵AC=6,△ACD是直角三角形,
∴AD2=AC2+CD2=62+32=45,
∴AD=3
| 5 |
点评:本题考查的是三角形的外接圆与外心,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果(ax-b)(x-3)=x2-9,那么( )
| A、a=1,b=3 |
| B、a=-1,b=-3 |
| C、a=1,b=-3 |
| D、a=-1,b=3 |
 如图,在△ABC中,DE为AC的垂直平分线,△BDC周长为6,AB-BC=2,求AB、BC的长.
如图,在△ABC中,DE为AC的垂直平分线,△BDC周长为6,AB-BC=2,求AB、BC的长. 如图,AB为⊙O的直径,C为半圆的中点,⊙C的半径为2,AB=8,点P是直径AB上的一动点,PM与⊙C切于点M,则PM的取值范围为
如图,AB为⊙O的直径,C为半圆的中点,⊙C的半径为2,AB=8,点P是直径AB上的一动点,PM与⊙C切于点M,则PM的取值范围为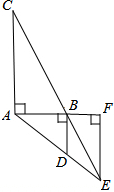 如图所示,CA⊥AB,DB⊥AB,AD与BC的延长线相交于点E,作EF⊥AB,交AB延长线于点F,且AC=p,BD=q,EF=r,AF=m,FB=n.求证:
如图所示,CA⊥AB,DB⊥AB,AD与BC的延长线相交于点E,作EF⊥AB,交AB延长线于点F,且AC=p,BD=q,EF=r,AF=m,FB=n.求证: 如图是由若干个大小相同的小正方体组成的几何体,从上面、左面、正面看会得到三个图形,其中看到的图形面积最小的是
如图是由若干个大小相同的小正方体组成的几何体,从上面、左面、正面看会得到三个图形,其中看到的图形面积最小的是