题目内容
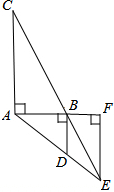 如图所示,CA⊥AB,DB⊥AB,AD与BC的延长线相交于点E,作EF⊥AB,交AB延长线于点F,且AC=p,BD=q,EF=r,AF=m,FB=n.求证:
如图所示,CA⊥AB,DB⊥AB,AD与BC的延长线相交于点E,作EF⊥AB,交AB延长线于点F,且AC=p,BD=q,EF=r,AF=m,FB=n.求证:| 1 |
| p |
| 1 |
| q |
| 1 |
| r |
考点:平行线分线段成比例
专题:证明题
分析:推出AC∥BD∥EF,求出△BDE∽△CAE,△FBE∽△ABC,得出比例式
=
=
,
=
,代入后相减即可求出
-
=
-
=1,推出即可.
| AC |
| BD |
| CE |
| BE |
| AF |
| BF |
| AC |
| EF |
| AB |
| BF |
| p |
| q |
| p |
| r |
| m |
| n |
| m-n |
| n |
解答:证明:∵CA⊥AB,DB⊥AB,EF⊥AB,
∴∠CAB=∠DBA=∠F=90°,
∴AC∥BD∥EF,
∴△BDE∽△CAE,△FBE∽△ABC,
∴
=
=
,
=
,
∵AC=p,BD=q,EF=r,AF=m,FB=n,
∴
=
,
=
,
∴
-
=
-
=1,
∴
-
=
,
∴
+
=
.
∴∠CAB=∠DBA=∠F=90°,
∴AC∥BD∥EF,
∴△BDE∽△CAE,△FBE∽△ABC,
∴
| AC |
| BD |
| CE |
| BE |
| AF |
| BF |
| AC |
| EF |
| AB |
| BF |
∵AC=p,BD=q,EF=r,AF=m,FB=n,
∴
| p |
| q |
| m |
| n |
| p |
| r |
| m-n |
| n |
∴
| p |
| q |
| p |
| r |
| m |
| n |
| m-n |
| n |
∴
| 1 |
| q |
| 1 |
| r |
| 1 |
| p |
∴
| 1 |
| p |
| 1 |
| q |
| 1 |
| r |
点评:本题考查了平行线分线段成比例定理,相似三角形的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
在△ABC和△FED中,如果∠A=∠F,∠B=∠E,要使这两个三角形全等,还需要的条件是( )
| A、AB=DE |
| B、BC=EF |
| C、AB=FE |
| D、∠C=∠D |
 如图,正方形ABCD的边长为8,点M在边DC上,且DM=2,M、N两点关于对角线AC对称,则tan∠ADN=
如图,正方形ABCD的边长为8,点M在边DC上,且DM=2,M、N两点关于对角线AC对称,则tan∠ADN=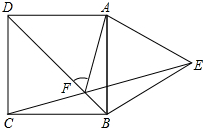 如图,四边形ABCD为正方形,以AB为边向正方形外作等边三角形ABE,CE与DB相交于点F,则
如图,四边形ABCD为正方形,以AB为边向正方形外作等边三角形ABE,CE与DB相交于点F,则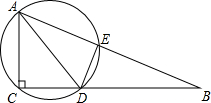 如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.
如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.