题目内容
如图，在△ABC中，DE为AC的垂直平分线，△BDC周长为6，AB-BC=2，求AB、BC的长．考点：线段垂直平分线的性质
专题：
分析：根据线段垂直平分线的性质可得DC=AD，进而可得AB+BC=6，再结合AB-BC=2，可解出AB、BC的长．
解答：解：∵DE为AC的垂直平分线，
∴DC=AD，
∵△BDC周长为6，
∴DC+BD+BC=6，
∴AB+BC=6，
∵AB-BC=2，
∴AB=4，BC=2．
∴DC=AD，
∵△BDC周长为6，
∴DC+BD+BC=6，
∴AB+BC=6，
∵AB-BC=2，
∴AB=4，BC=2．
点评：此题主要考查了线段垂直平分线的性质，关键是掌握垂直平分线上任意一点，到线段两端点的距离相等．
练习册系列答案
相关题目
如图，正方形ABCD的边长为8，点M在边DC上，且DM=2，M、N两点关于对角线AC对称，则tan∠ADN=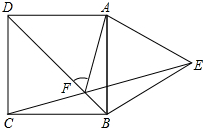
如图，四边形ABCD为正方形，以AB为边向正方形外作等边三角形ABE，CE与DB相交于点F，则
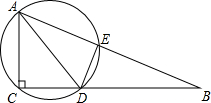如图，在Rt△ABC中，∠ACB=90°，AC=6，CB=8，AD是△ABC的角平分线，过A，D，C三点的圆与斜边AB交于点E，连接DE．在△ABC和△FED中，如果∠A=∠F，∠B=∠E，要使这两个三角形全等，还需要的条件是（ ）
| A、AB=DE |
| B、BC=EF |
| C、AB=FE |
| D、∠C=∠D |