题目内容
17.四个连续整数的和为S,S满足不等式15<$\frac{S}{2}$<19.这四个数中最大数与最小数的平方差等于51.分析 先解不等式15<$\frac{S}{2}$<19,得到S的取值范围为30<S<38,根据S为四个连续整数的和,可得四个连续整数为7,8,9,10,进一步求得这四个数中最大数与最小数的平方差即可求解.
解答 解:∵15<$\frac{S}{2}$<19,
∴30<S<38,
∵S为四个连续整数的和,
∴四个连续整数为7,8,9,10,
∴102-72=100-49=51.
故这四个数中最大数与最小数的平方差等于51.
故答案为:51.
点评 考查了一元一次不等式的整数解,解题的关键和难点是根据S的取值范围得到四个连续整数为7,8,9,10.

练习册系列答案
相关题目
6.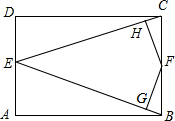 如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
 如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{2}$$\sqrt{10}$ | C. | $\frac{3}{10}$$\sqrt{10}$ | D. | $\frac{3}{5}$$\sqrt{10}$ |
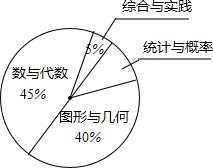 在结束了初中阶段数学内容的新课教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制了如图所示的扇形统计图,则唐老师安排复习“统计与概率”内容的时间为6课时.
在结束了初中阶段数学内容的新课教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制了如图所示的扇形统计图,则唐老师安排复习“统计与概率”内容的时间为6课时.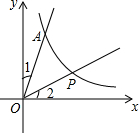 如图,直线y=3x和双曲线y=$\frac{3}{x}$(x>0)交于点A,点P为双曲线上一点,且∠POA=∠1+∠2,求点P的坐标.
如图,直线y=3x和双曲线y=$\frac{3}{x}$(x>0)交于点A,点P为双曲线上一点,且∠POA=∠1+∠2,求点P的坐标.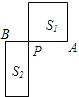 如图,线段AB=1,P是AB的黄金分割点,且PA>PB,S1表示以PA为边长的正方形面积,S2表示以AB为长、PB为宽的矩形面积,则S1-S2=0.
如图,线段AB=1,P是AB的黄金分割点,且PA>PB,S1表示以PA为边长的正方形面积,S2表示以AB为长、PB为宽的矩形面积,则S1-S2=0.