题目内容
12. 如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是2.
如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是2.
分析 设AC=x,BC=4-x,根据等腰直角三角形性质,得出CD=$\frac{\sqrt{2}}{2}$x,CE=$\frac{\sqrt{2}}{2}$(4-x),根据勾股定理然后用配方法即可求解.
解答 解:设AC=x,BC=4-x,
∵△CD,△BCE均为等腰直角三角形,
∴CD=$\frac{\sqrt{2}}{2}$x,CE=$\frac{\sqrt{2}}{2}$(4-x),
∵∠ACD=45°,∠BCE=45°,
∴∠DCE=90°,
∴DE2=CD2+CE2=$\frac{1}{2}$x2+$\frac{1}{2}$(4-x)2=x2-4x+8=(x-2)2+4,
∵根据二次函数的最值,
∴当x取2时,DE取最小值,最小值为:2.
故答案为:2
点评 本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
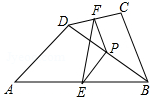 如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是120°.
如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是120°. 如图,在△ABC中,点D在BC上且AB=AD,AC=AE,∠BAD=∠CAE,DE=12,CD=4,则BD=8.
如图,在△ABC中,点D在BC上且AB=AD,AC=AE,∠BAD=∠CAE,DE=12,CD=4,则BD=8.