题目内容
17.在等腰三角形ABC中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即T(A)=$\frac{∠A的对边(底边)}{∠A的邻边(腰)}$=$\frac{BC}{AB}$.例:T(60°)=1,那么T(120°)=$\sqrt{3}$.分析 根据T(A)的定义解答即可.
解答  解:∠BAC=90°,AB=AC,作AD⊥BC于D,则∠BAD=60°,
解:∠BAC=90°,AB=AC,作AD⊥BC于D,则∠BAD=60°,
∴BD=$\frac{\sqrt{3}}{2}$AB,
∴BC=$\sqrt{3}$AB,
∴T(120°)=$\sqrt{3}$.
故答案是:$\sqrt{3}$.
点评 本题考查了解直角三角形,正确理解T(A)的定义是解题的关键.

练习册系列答案
相关题目
8.小明每秒钟跑6米,小彬每秒钟跑5米,小彬站在小明前10米处,两人同时起跑,小明用( )秒钟追上小彬.
| A. | 5 秒 | B. | 6秒 | C. | 8 秒 | D. | 10秒 |
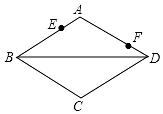 如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为4.
如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为4.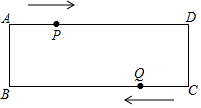 如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB?
如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB? 如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是2.
如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是2.