题目内容
20.按要求完成下列尺规作图(不写作图,保留作图痕迹).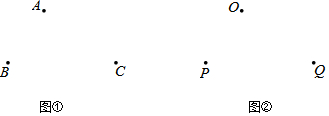
(1)如图①,点A、B、C是平行四边形ABCD的三个顶点,求作平行四边形ABCD;
(2)如图②,点O、P、Q分别是平行四边形EFGH三边EH、EF、FG的中点,求作平行四边形EFGH.
分析 (1)分别以A、C点为圆心,BC和AB为半径画弧相交于点D,则利用平行四边形的判定方法可判断四边形ABCD满足条件;
(2)利用(1)中的方法先以O、P、Q三点画平行四边形OPQK,对角线相交于点O,然后再分别画平行四边形可得到满足条件的四边形EFGH.
解答 解:(1)如图①,四边形ABCD即为所求;
(2)如图②,四边形EFGH即为所求.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行四边形的判定与性质.

练习册系列答案
相关题目
8.下列等式一定成立的是( )
| A. | $\sqrt{9}$-$\sqrt{4}$=$\sqrt{5}$ | B. | |1-$\sqrt{3}$|=$\sqrt{3}$-1 | C. | $\sqrt{9}$=±3 | D. | -$\sqrt{(-9)^{2}}$=9 |
12.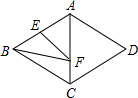 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
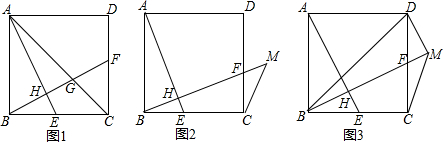
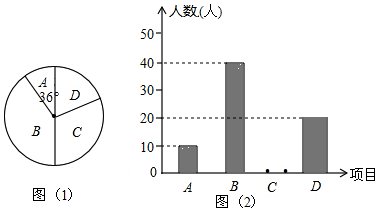
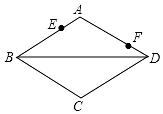 如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为4.
如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为4.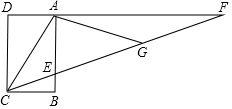 “三等分一个任意角”是数学史上一个著名问题,今天人们已经知道,仅用圆规直尺是不可能做出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是长方形(AD∥CB),F是DA延长线上一点,G 是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F,你能证明∠ECB=$\frac{1}{3}$∠ACB吗?
“三等分一个任意角”是数学史上一个著名问题,今天人们已经知道,仅用圆规直尺是不可能做出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是长方形(AD∥CB),F是DA延长线上一点,G 是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F,你能证明∠ECB=$\frac{1}{3}$∠ACB吗? 如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是2.
如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是2.