题目内容
4.根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:若a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,则a<b.反之也成立.这种比较大小的方法称为“求差法比较大小”.请运用这种方法尝试解决下面的问题:
(1)比较4+3a2-2b+b2与3a2-2b+1的大小;
(2)若2a+2b-1>3a+b,则a、b的大小关系(直接写出答案).
分析 根据作差法,差大于零被减数大,差小于零被减数小,可得答案.
解答 解:(1)4+3a2-2b+b2-(3a2-2b+1)
=b2+3>0,
∴4+3a2-2b+b2>3a2-2b+1;
(2)两边都减(3a+b),得
-a+b-1>0,
b-a>1,
∴a<b.
点评 本题考查了实数大小比较,利用作差法,差大于零被减数大,差小于零被减数小是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.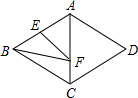 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )
如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
 如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是2.
如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是2.
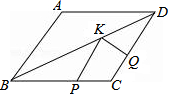 如图,菱形ABCD中,AB=3,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为$\frac{3\sqrt{3}}{2}$.
如图,菱形ABCD中,AB=3,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为$\frac{3\sqrt{3}}{2}$.