题目内容
5.化简:(1)$\frac{a-b}{\sqrt{a}-\sqrt{b}}$;
(2)$\frac{\sqrt{a+2}+\sqrt{a-2}}{\sqrt{a+2}-\sqrt{a-2}}$.
分析 (1)利用平方差公式把分子a-b变形,然后约分即可;
(2)分母有理化即可.
解答 解:(1)原式=$\frac{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}{(\sqrt{a}-\sqrt{b})}$
=$\sqrt{a}$+$\sqrt{b}$;
(2)原式=$\frac{(\sqrt{a+2}+\sqrt{a-2})^{2}}{(\sqrt{a+2}-\sqrt{a-2})(\sqrt{a+2}-\sqrt{a-2})}$
=$\frac{a+2+2\sqrt{{a}^{2}-4}+a-2}{a+2-(a-2)}$
=$\frac{a+\sqrt{{a}^{2}-4}}{2}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
16.若圆锥的侧面展开图是个半圆,则该圆锥的侧面积与全面积之比为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
20.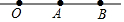 如图,O,A,B三点在同一直线上,则下列说法中正确的是( )
如图,O,A,B三点在同一直线上,则下列说法中正确的是( )
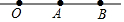 如图,O,A,B三点在同一直线上,则下列说法中正确的是( )
如图,O,A,B三点在同一直线上,则下列说法中正确的是( )| A. | 射线OA与射线AO表示同一条射线 | B. | 射线OA大于射线AB | ||
| C. | 射线OA与射线OB表示同一条射线 | D. | 线段OA与线段AO表示两条不同线段 |
6.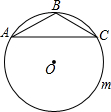 如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
 如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )| A. | y=$\frac{\sqrt{3}}{4}$x+4 | B. | y=$\sqrt{3}$x+4 | C. | y=$\sqrt{3}$x2+4 | D. | y=$\frac{\sqrt{3}}{4}$x2+4 |
4.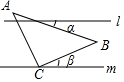 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
 如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )
如图,直线l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
