题目内容
在△ABO中,OA=OB=2cm,⊙O的半径为1cm,当∠ABO= °时,直线AB与⊙O相切.
考点:切线的判定
专题:
分析:如图,作辅助线;证明OC⊥AB;运用直角三角形的性质,求出∠A,即可解决问题.
解答: 解:如图,连接OC,
解:如图,连接OC,
∵⊙O与直线AB相切于点C;
∴OC⊥AB;而OA=2,OC=1,
∴∠A=30°;而OA=OB,
∴∠B=∠A=30°,
∴∠AOB=180°-60°=120°,
故答案为120.
 解:如图,连接OC,
解:如图,连接OC,∵⊙O与直线AB相切于点C;
∴OC⊥AB;而OA=2,OC=1,
∴∠A=30°;而OA=OB,
∴∠B=∠A=30°,
∴∠AOB=180°-60°=120°,
故答案为120.
点评:该题主要考查了圆的切线的判定、等腰三角形的性质及其应用问题;牢固掌握切线的判定、等腰三角形的性质是解题的基础和关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
下列计算正确的是( )
| A、(2x+3y)2=4x2+9y2 | ||||||||||
B、(-c+
| ||||||||||
C、(
| ||||||||||
| D、(2a+5b)2=4a2+10ab+25b2 |

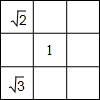 如图,试在图中填上恰当的数,使得图中每一行,每一列,每条对角线上3个数的乘积都等于1,你还能找到一个数,使得图中每一行,每一列,每一条对角线上3个数的乘积都等于这个数吗?
如图,试在图中填上恰当的数,使得图中每一行,每一列,每条对角线上3个数的乘积都等于1,你还能找到一个数,使得图中每一行,每一列,每一条对角线上3个数的乘积都等于这个数吗?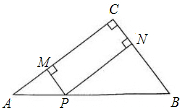 如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足分别为M、N,设AP=x.
如图,在△ABC中,∠C=90°,AC=8,BC=6,P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足分别为M、N,设AP=x. 有理数a、b、c在数轴上的对应点如图,化简代数式:|a-b|+|a+b|-|c-a|+2|b-c|.
有理数a、b、c在数轴上的对应点如图,化简代数式:|a-b|+|a+b|-|c-a|+2|b-c|.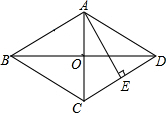 在菱形ABCD中,对角线AC与BD相交于点O,AE⊥CD于点E,且AE=OD,求∠ADC的度数.
在菱形ABCD中,对角线AC与BD相交于点O,AE⊥CD于点E,且AE=OD,求∠ADC的度数.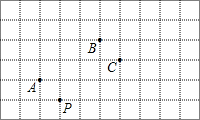 如图,在每个小方格都是正方形的网格中,一颗棋子从P点开始依次关于点A,B,C作循环对称跳动,即第一次跳到P点关于A点的对称点M处,第二次跳到M点关于B点的对称点N处,第三次跳到N点关于C点的对称点处,…,以此类推,循环往复,经过2015次跳动后,距离棋子落点最近的点是( )
如图,在每个小方格都是正方形的网格中,一颗棋子从P点开始依次关于点A,B,C作循环对称跳动,即第一次跳到P点关于A点的对称点M处,第二次跳到M点关于B点的对称点N处,第三次跳到N点关于C点的对称点处,…,以此类推,循环往复,经过2015次跳动后,距离棋子落点最近的点是( )