题目内容
3．在函数y=（x-3）2中，当x＞3时，函数值y随x的增大而增大；当x＜3时，函数值y随x的增大而减；当x=3时，函数值y取最小值，是0．分析 由抛物线解析式可知，抛物线开口向上，顶点坐标为（3，0），对称轴为x=3，由此判断增减性和最值．
解答 解：∵函数y=（x-3）2的对称轴为x=3，顶点为（3，0），
又∵二次函数开口向上，
∴x＞3时，y随x增大而增大，x＜3时，y随x增大而减小，当x=3时，函数y取最小值，最小值为0．
故答案为：＞3，＜3，3，小，0．
点评 本题考查了二次函数的性质．关键是根据开口方向及对称轴判断函数的增减性，根据开口方向和顶点坐标判断函数的最值．
练习册系列答案
阅读快车系列答案
相关题目
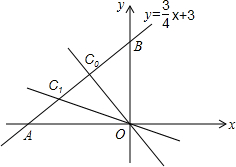一次函数y=$\frac{3}{4}$x+m的图象过点（4，6），且分别与x轴、y轴交于A、B点，点P（a，0）在x轴正半轴上运动，点Q（0，b）在y轴正半轴上运动．