题目内容
11.已知Rt△ABC中,∠C=90°,BC=10,AB=40.解这个直角三角形(角精确到1°).分析 首先根据勾股定理推出AC的长度,然后根据AC和AB的关系即可推出∠B的度数,既而求出∠A的度数.
解答 解:在Rt△ABC中,∠C=90°,BC=10,AB=40,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=10$\sqrt{15}$,
∴sinA=$\frac{BC}{AB}$=0.25,
∴∠A≈15°,
∴∠B=90°-∠A=75°.
点评 此题主要考查了解直角三角形,熟练应用计算器是解题关键.

练习册系列答案
相关题目
1.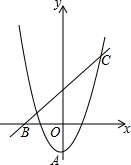 如图,抛物线y=2x2-1与直线y=x+2交于B、C两点,抛物线顶点为A,则△ABC的面积为( )
如图,抛物线y=2x2-1与直线y=x+2交于B、C两点,抛物线顶点为A,则△ABC的面积为( )
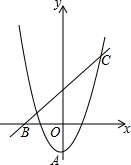 如图,抛物线y=2x2-1与直线y=x+2交于B、C两点,抛物线顶点为A,则△ABC的面积为( )
如图,抛物线y=2x2-1与直线y=x+2交于B、C两点,抛物线顶点为A,则△ABC的面积为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{8}$ | C. | $\frac{7}{2}$ | D. | $\frac{5}{2}$ |
6.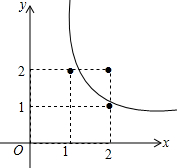 如图,已知反比例函数y=$\frac{k}{x}$(x>0),则k的取值范围是( )
如图,已知反比例函数y=$\frac{k}{x}$(x>0),则k的取值范围是( )
 如图,已知反比例函数y=$\frac{k}{x}$(x>0),则k的取值范围是( )
如图,已知反比例函数y=$\frac{k}{x}$(x>0),则k的取值范围是( )| A. | 1<k<2 | B. | 2<k<3 | C. | 2<k<4 | D. | 2≤k≤4 |
1.下列方程中,解是x=$\frac{2}{3}$的方程是( )
| A. | x+2x=-2 | B. | 5x-11x=-4 | C. | 7x-5x=3 | D. | -$\frac{1}{3}$x+x=-1 |
 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象. 数轴上A、B(A左B右)所对应的数为a,b,|a+5|+(b-10)2=0,C为数轴上一动点且对应的数为c,O为原点.
数轴上A、B(A左B右)所对应的数为a,b,|a+5|+(b-10)2=0,C为数轴上一动点且对应的数为c,O为原点.