题目内容
2.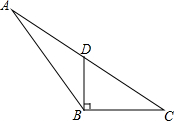 如图,在△ABC中,D为边AC的中点,且DB⊥BC,BC=4,CD=5.
如图,在△ABC中,D为边AC的中点,且DB⊥BC,BC=4,CD=5.(1)求DB的长;
(2)在△ABC中,求边BC上的高.
【友情提示】辅助定理:△ABC中,D为AB中点,且DE∥BC交AC于E,则DE∥BC,且DE=$\frac{1}{2}$BC.
分析 (1)直接利用勾股定理得出BD的长即可;
(2)利用三角形中位线定理得到AE的长度即可.
解答  解:(1)∵DB⊥BC,
解:(1)∵DB⊥BC,
∴∠DBC=90°.
在Rt△DBC中,BC=4,CD=5,
∴DB=$\sqrt{C{D}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3;
(2)过A作AE⊥BC交线段CB延长线于E,
∵DB⊥BC,
∴AE∥DB.
∵D为AC的中点,
∴DB为△ACE的中位线.
∴AE=2DB=6.
∴边BC上的高为6.
点评 此题主要考查了勾股定理,三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.

练习册系列答案
相关题目
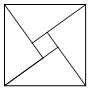 2002年8月,在北京召开国际数学家大会,大会的会标取材于我国古代数学家赵爽的《勾股圆方图》.其中的“弦图”是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,如图所示.如果直角三角形的直角边分别为a,b(a>b),斜边为c,那么小正方形的面积可以表示为c2-2ab.
2002年8月,在北京召开国际数学家大会,大会的会标取材于我国古代数学家赵爽的《勾股圆方图》.其中的“弦图”是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,如图所示.如果直角三角形的直角边分别为a,b(a>b),斜边为c,那么小正方形的面积可以表示为c2-2ab. 如图,在△ABC中,AB=AC,BC=20cm,D是AB上一点,且CD=16cm,BD=12cm.
如图,在△ABC中,AB=AC,BC=20cm,D是AB上一点,且CD=16cm,BD=12cm.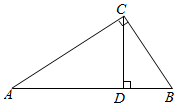 如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,AC=2,CD=1,则线段BC=$\frac{2\sqrt{3}}{3}$.
如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,AC=2,CD=1,则线段BC=$\frac{2\sqrt{3}}{3}$.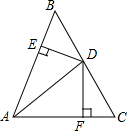 如图,在△ABC中,AD平分∠CAB,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:AD⊥BC.
如图,在△ABC中,AD平分∠CAB,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:AD⊥BC.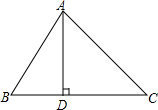 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.