题目内容
14.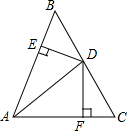 如图,在△ABC中,AD平分∠CAB,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:AD⊥BC.
如图,在△ABC中,AD平分∠CAB,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:AD⊥BC.
分析 根据角平分线上的点到角的两边距离相等可得DE=DF,然后利用“HL”证明Rt△BDE和Rt△CDF全等,根据全等三角形对应角相等可得∠B=∠C,根据等角对等边可得AB=AC,再利用等腰三角形三线合一的性质证明即可.
解答 证明:∵AD平分∠CAB,DE⊥AB,DF⊥AC,
∴DE=DF,
∵D为BC的中点,
∴BD=CD,
在Rt△BDE和Rt△CDF中,$\left\{\begin{array}{l}{BD=CD}\\{DE=DF}\end{array}\right.$,
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C,
∴AB=AC,
又∵D为BC的中点,
∴AD⊥BC.
点评 本题考查了全等三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,等腰三角形三线合一的性质,熟记各性质以及三角形全等的判定方法熟记解题的关键.

练习册系列答案
相关题目
9.用直接开平方法解下列一元二次方程,其中无解的方程为( )
| A. | x2-1=0 | B. | x2=0 | C. | x2+4=0 | D. | -x2+3=0 |
19. 一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°.若AB=4,则S△BCD=$\frac{3\sqrt{3}-3}{2}$(结果保留根号)
一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°.若AB=4,则S△BCD=$\frac{3\sqrt{3}-3}{2}$(结果保留根号)
 一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°.若AB=4,则S△BCD=$\frac{3\sqrt{3}-3}{2}$(结果保留根号)
一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°.若AB=4,则S△BCD=$\frac{3\sqrt{3}-3}{2}$(结果保留根号)
6.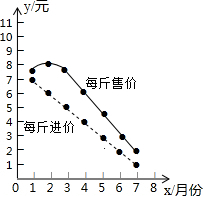 1-7月份,某种蔬菜每斤的进价与每斤的售价的信息如图所示,则出售该种蔬菜每斤利润最大的月份是( )
1-7月份,某种蔬菜每斤的进价与每斤的售价的信息如图所示,则出售该种蔬菜每斤利润最大的月份是( )
 1-7月份,某种蔬菜每斤的进价与每斤的售价的信息如图所示,则出售该种蔬菜每斤利润最大的月份是( )
1-7月份,某种蔬菜每斤的进价与每斤的售价的信息如图所示,则出售该种蔬菜每斤利润最大的月份是( )| A. | 3月份 | B. | 4月份 | C. | 5月份 | D. | 6月份 |
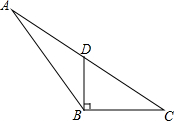 如图,在△ABC中,D为边AC的中点,且DB⊥BC,BC=4,CD=5.
如图,在△ABC中,D为边AC的中点,且DB⊥BC,BC=4,CD=5.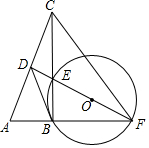 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线交于点D、E、F,且BF=BC,⊙O是△BEF的外接圆,连接BD.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线交于点D、E、F,且BF=BC,⊙O是△BEF的外接圆,连接BD.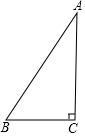 如图,△ABC中,∠C=90°.
如图,△ABC中,∠C=90°.