题目内容
17.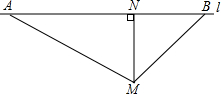 如图,根据道路管理规定,在某笔直的大道AB上行驶的车辆,限速60千米/时,已知测速站点M距大道AB的距离MN为30米,现有一辆汽车从A向B方向匀速行驶,测得此车从A点行驶到B点所用时间危机6秒,∠AMN=60°,∠BMN=45°.
如图,根据道路管理规定,在某笔直的大道AB上行驶的车辆,限速60千米/时,已知测速站点M距大道AB的距离MN为30米,现有一辆汽车从A向B方向匀速行驶,测得此车从A点行驶到B点所用时间危机6秒,∠AMN=60°,∠BMN=45°.(1)计算AB的长度(结果保留整数).
(2)通过计算判断此车是否超速.(温馨提示:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 (1)已知MN=30m,∠AMN=60°,∠BMN=45°求AB的长度,可以转化为解直角三角形;
(2)求得从A到B的速度,然后与60千米/时≈16.66米/秒,比较即可确定答案.
解答 解:(1)在Rt△AMN中,MN=30,∠AMN=60°,
∴AN=MN•tan∠AMN=30$\sqrt{3}$.
在Rt△BMN中,
∵∠BMN=45°,
∴BN=MN=30.
∴AB=AN+BN=(30+30$\sqrt{3}$)米;
(2)∵此车从A点行驶到B点所用时间为6秒,
∴此车的速度为:(30+30$\sqrt{3}$)÷6=5+5$\sqrt{3}$≈13.66,
∵60千米/时≈16.66米/秒,
∴13.66<16.66
∴不会超速.
点评 本题考查了勾股定理以及解直角三角形的应用,解题的关键是从题目中抽象出直角三角形,难度不大.

练习册系列答案
相关题目
5.在2,-2,0,-3中,最大的数是( )
| A. | 2 | B. | -2 | C. | 0 | D. | -3 |
12.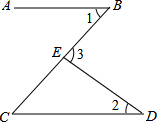 如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
 如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )| A. | 80° | B. | 70° | C. | 90° | D. | 100° |
6.数据9、9、6、3、6、2、6的众数是( )
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
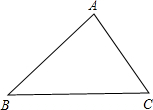 将△ABC沿BC方向平移,使点B移到点C
将△ABC沿BC方向平移,使点B移到点C