题目内容
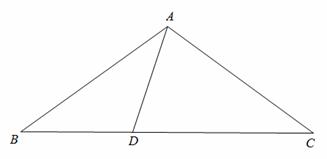
如图,已知△ABC,AB=AC=1,∠BAC=108°,点D在BC上,AD=BD,则AD的长是
,cosB的值是 (结果保留根号)。
 ;
; 。
。
【考点】等腰三角形的性质,三 角形内角和定理,相似三角形的判定和性质,锐角三角函数的定义。
角形内角和定理,相似三角形的判定和性质,锐角三角函数的定义。
【分析】可以证明△ ABC∽△BDA,设AD=x,根据相似三角形的对应边的比相等,即可列出方程,求得x
ABC∽△BDA,设AD=x,根据相似三角形的对应边的比相等,即可列出方程,求得x 的值;过点D作DE⊥AB于点E,则E为AB中点,由余弦定义可求出cosB的值:
的值;过点D作DE⊥AB于点E,则E为AB中点,由余弦定义可求出cosB的值:
∵ 在△ABC中,AB=AC=1,∠BAC=108°,∴ ∠ABC=∠ACB=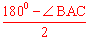 =36
=36 °。
°。
∵AD=BD,∴∠ABD=∠BAD=36°。∴ △ABC∽△BDA。∴  。
。
∵∠BAC=108°,∠BAD=36°,∴∠CAD=72°。
又∵∠ACB=36°,∴∠CDA=72°。∴∠CAD=∠CDA=72°。∴CD=CA=1。
设A D=x,则BD=AD=x,BC=
D=x,则BD=AD=x,BC=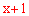 ,
,
∴ (舍去负值)。
(舍去负值)。
∴AD=x= 。
。



练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 园,决定从某苗圃购进甲、乙、丙三种树苗共80株,其中甲种树苗株树是乙种树苗株树的2倍,购买三种树苗的总金额不超过1320元,已知乙种树苗的单价是16元/
园,决定从某苗圃购进甲、乙、丙三种树苗共80株,其中甲种树苗株树是乙种树苗株树的2倍,购买三种树苗的总金额不超过1320元,已知乙种树苗的单价是16元/ 株,乙种树苗的单价是甲种树苗的单价的
株,乙种树苗的单价是甲种树苗的单价的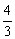 ,购买丙种树苗12株的金额等于购买甲种树
,购买丙种树苗12株的金额等于购买甲种树 苗20株的金额。
苗20株的金额。 甲、丙两种树苗的单价分别是多少元?
甲、丙两种树苗的单价分别是多少元? 树苗的株树不超过丙种树苗的株树,请你帮助设计共有哪些购买方案?
树苗的株树不超过丙种树苗的株树,请你帮助设计共有哪些购买方案?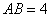
 ,点
,点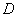
 的坐标是
的坐标是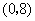
 ,以点
,以点
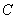
 为顶点的抛物线
为顶点的抛物线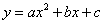
 经过
经过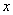
 轴上的点
轴上的点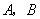
 .
.

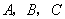
 的坐标;
的坐标; 正六边形靶子上随意抛一枚飞镖,则飞镖插不落在阴影区域的概率为【 】
正六边形靶子上随意抛一枚飞镖,则飞镖插不落在阴影区域的概率为【 】
 B.
B.  C.
C.  D.
D. 
 ,AC=
,AC= ,BC=6,点M在AB边上,且AM=
,BC=6,点M在AB边上,且AM= BM,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长。
BM,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长。

 P于点P(图2),试求AE与EP的数量关系;
P于点P(图2),试求AE与EP的数量关系;
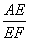
 =3,求
=3,求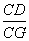
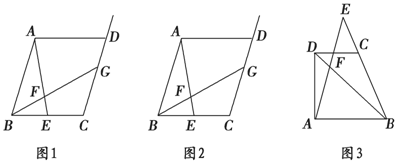

 :
:

 在Rt△ABC中,∠C=900,∠B=300,BC=
在Rt△ABC中,∠C=900,∠B=300,BC=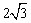 ,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直
,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直 线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为 。
线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为 。
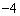 )两点。
)两点。