题目内容
如图1,矩形ABCD中,AB=6,BC=8,点E、F分别是BC、CD边上的点,且AE⊥EF,BE=2,
(1)求证:AE=EF;
(2)延长EF交矩形∠BCD的外角平分线C
 P于点P(图2),试求AE与EP的数量关系;
P于点P(图2),试求AE与EP的数量关系;

(1)∵AE⊥EF,∴∠BEA+∠CEF=90°。
∵四边形ABCD为矩 形,∴∠B=∠C=90°。
形,∴∠B=∠C=90°。
∴∠BAE +∠BEA =90°。∴∠BA E=∠CEF。
又∵AB=DC=6,BC=8,BE=2,∴AB=EC=6。
∴△ABE≌△ECF(ASA)。
∴AE=EF。
(2)如图,在AB上取一点M,使BM=BE, 连接ME。
连接ME。

∴A M=CE。
M=CE。 ∴∠BME=45°。∴∠AME=135°。
∴∠BME=45°。∴∠AME=135°。
∵CP是外角平分线,∴∠ DCP=45°。∴∠ECP=135°。
DCP=45°。∴∠ECP=135°。
∴∠AME=∠ECP。
由(1)知∠MA E=∠CEP ,
,
∴△AME∽△ECP。∴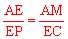 。
。
∵AM=2,EC=3,∴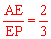 。
。
∴AE与EP的数量关系是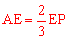 。
。
【考点】矩形的 性质,全等三角形的判定和性质,外角平分线定义
性质,全等三角形的判定和性质,外角平分线定义 ,相似三角形的判定和性质。
,相似三角形的判定和性质。


练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 8cm.点D、E、F分别是
8cm.点D、E、F分别是 边AB,BC,AC的中点,连接DE,DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止;
边AB,BC,AC的中点,连接DE,DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止; 点Q沿BC的方向运动,当点P停止运动时
点Q沿BC的方向运动,当点P停止运动时 也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQ
也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQ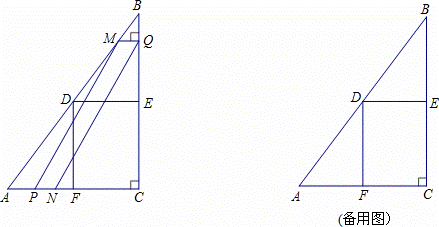
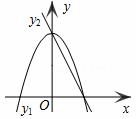
 2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2
2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2 ,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断:
,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断: x<0时,y1>y2;
x<0时,y1>y2; 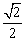 。
。

 知⊙B与△ABD的边A
知⊙B与△ABD的边A D相切于点C,AC=
D相切于点C,AC= ,⊙B的半径为2,当⊙A与⊙B相切时,⊙A
,⊙B的半径为2,当⊙A与⊙B相切时,⊙A 的半径是【 】
的半径是【 】
 1
1  3
3  2
2 1或3
1或3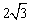 ,经过O,C两点做抛物线
,经过O,C两点做抛物线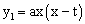 (a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)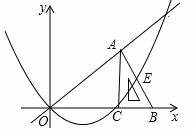
 线
线 的顶点在函数
的顶点在函数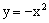 的图象上;
的图象上; 的值。
的值。