题目内容
2.将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动$\frac{2}{3}$秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).(1)求点B的坐标,并用含t的代数式表示OP,OQ;
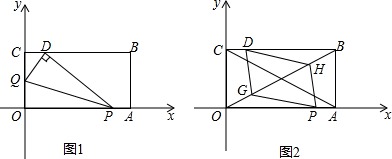
(2)当t=1时,如图1,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D的坐标;
(3)在(2)的条件下,矩形对角线AC,BO交于M,取OM中点G,BM中点H,求证:当t=1时四边形DGPH是平行四边形.
分析 (1)由O(0,0),A(6,0),C(0,3),可得:OA=6,OC=3,根据矩形的对边平行且相等,可得:AB=OC=3,BC=OA=6,进而可得点B的坐标为:(6,3),然后根据P点与Q点的运动速度与运动时间即可用含t的代数式表示OP,OQ;
(2)由翻折的性质可知:△OPQ≌△DPQ,进而可得:DQ=OQ,然后由t=1时,DQ=OQ=$\frac{5}{3}$,CQ=OC-OQ=$\frac{4}{3}$,然后利用勾股定理可求CD的值,进而可求点D的坐标;
(3)由(1),(2)知:当t=1时,CD=AP=1,OA=BC=6,进而可得:BD=OP=5,然后由矩形的性质可得:OG=BH,∠CBO=∠AOB,然后根据SAS证明△POG≌△DBH,进而可得PG∥DH,PG=DH,然后根据一组对边平行且相等的四边形是平行四边形,即可求证:当t=1时四边形DGPH是平行四边形.
解答 (1)解:∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点Q从O点以每秒1个单位长的速度沿OC向终点C运动,运动$\frac{2}{3}$秒时,动点P从点A出发以相等的速度沿AO向终点O运动.
∴当点P的运动时间为t(秒)时,
AP=t,OQ=$\frac{2}{3}$+t,
则OP=OA-AP=6-t;
(2)解:当t=1时,OQ=$\frac{5}{3}$,则CQ=CQ=OC-OQ=$\frac{4}{3}$,
由折叠可知:△OPQ≌△DPQ,
∴OQ=DQ=$\frac{5}{3}$,
由勾股定理,得:CD=1,
∴D(1,3);
(3)证明:如图所示,
由(1),(2)知:当t=1时,
CD=AP=1,OA=BC=6
∴BC-CD=OA-AP,即BD=OP=5,
∵四边形OABC是矩形,
∴OM=MB,OA∥BC,
∵G为OM中点,H为BM中点,
∴OG=BH,
∵OA∥BC,
∴∠CBO=∠AOB,
在△POG和△DBH中,
∵$\left\{\begin{array}{l}{BD=OP}\\{∠CBO=∠AOB}\\{BH=OG}\end{array}\right.$,
∴△POG≌△DBH(SAS),
∴∠OGP=∠BHD,PG=DH,
∴∠MGP=∠DHM,
∴PG∥DH,
∵PG=DH,
∴四边形DGPH是平行四边形.
故当t=1时四边形DGPH是平行四边形.
点评 此题是四边形的综合题,主要考查了动点的问题、矩形的性质、平行四边的判定、全等三角形的判定与性质等知识,解(1)的关键是:明确矩形的对边相等;解(2)的关键是:由翻折的性质可知:△OPQ≌△DPQ;解(3)的关键是:根据SAS证明△POG≌△DBH.

| A. | 2.5×10-8 | B. | 2.5×10-9 | C. | 2.5×10-10 | D. | 2.5×109 |
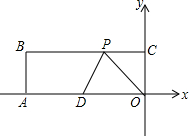 如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(-10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是(-4,3),或(-1,3),或(-9,3).
如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(-10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是(-4,3),或(-1,3),或(-9,3).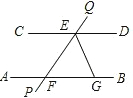 如图,AB∥CD,直线PQ分别交AB、CD于点E、F,EG是∠FED的平分线,交AB于点G.若∠QED=40°,那么∠EGB等于110°.
如图,AB∥CD,直线PQ分别交AB、CD于点E、F,EG是∠FED的平分线,交AB于点G.若∠QED=40°,那么∠EGB等于110°.