已知:$\sqrt{2}$cos=1.则sinx的值是( )A．$\frac{\sqrt{2}}{2}$B．$\frac{1}{2}$C．$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{3}}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

18．已知：$\sqrt{2}$cos（x+15°）=1，则sinx的值是（　　）

A．

$\frac{\sqrt{2}}{2}$

B．

$\frac{1}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

$\frac{\sqrt{3}}{3}$

分析已知等式变形，利用特殊角的三角函数值求出x的值，即可确定出sinx的值．

解答解：∵$\sqrt{2}$cos（x+15°）=1，即cos（x+15°）=$\frac{\sqrt{2}}{2}$，
∴x+15°=45°，即x=30°，
则sinx=sin30°=$\frac{1}{2}$，
故选：B．

点评此题考查了特殊角的三角函数值，牢记特殊角的三角函数值是解本题的关键．

练习册系列答案

相关题目

6．

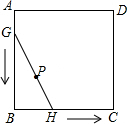如图，正方形ABCD的边长为4，线段GH=AB，将GH的两端放在正方形的相邻的两边上同时滑动，如果G点从A点出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时点H从点B出发，沿图中所示方向按B→C→D→A→B滑动到B止，在这个过程中，线段GH的中点P所经过的路线围成的图形的面积为16-4π．

9．二次函数y=x²-2x+3与一次函数y=x+1的图象相交吗？若相交，请求出交点坐标．

6．若一次函数y=（3a-2）x+6随着x的增大而增大，则a的取值范围是a＞$\frac{2}{3}$．

3．如果一次函数y=kx-b的图象经过第一、二、三象限，那么k的取值范围是（　　）

10．

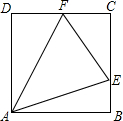如图，已知正方形ABCD的边长为1，点E，F分别在边BC，CD上，且∠EAF=45°，则△CEF的周长为2．

7．

如图，AB为⊙O的直径，AB=2，点在M在QO上，MC垂直平分OA，点N为直线AB上一动点（N不与A重合），若△MNP∽△MAC，PC与直线AB所夹锐角为α．
（1）若AM=AC，点N与点O重合，则α=30°；
（2）若点C、点N的位置如图所示，求α的度数；
（3）当直线PC与⊙O相切时，则MC的长为$\frac{4\sqrt{3}}{3}$．

8．

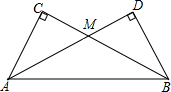把两个同样大小的含30°角的三角尺像如图所示那样放置，其中M是AD与BC的交点．
（1）此时MC的长度等于点M到AB的距离，请说明理由．
（2）图中除同样大小的三角尺外，你还能找出全等的三角形吗？如果能，请写出来并说明理由．

试题分类