题目内容
已知关于x的方程x2﹣(2m+1)x+m(m+1)=0,
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2,求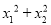 的最小值.
的最小值.
练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
题目内容
已知关于x的方程x2﹣(2m+1)x+m(m+1)=0,
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2,求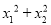 的最小值.
的最小值.
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案