题目内容
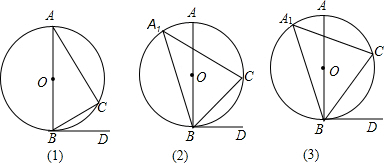
16.如图,已知AB是⊙O的直径,C为圆周上一点,BD是⊙O的切线,B为切点.(1)在图(1)中,∠BAC=30°,求∠DBC的度数;
(2)在图(2)中,∠BA1C=40°,求∠DBC的度数;
(3)在图(3)中,∠BA1C=α,求∠DBC大小.
分析 (1)由切线的性质和圆周角定理以及角的互余关系得出∠DBC=∠A=30°即可;
(2)连接AC,由(1)得出∠DBC=∠A,由圆周角定理得出∠A=∠A1,即可得出∠DBC=∠BA1C=40°;
(3)由(2)得出∠DBC=∠BA2C=α即可.
解答 解:(1)∵BD是⊙0的切线,
∴∠ABO=90°,
即∠ABC+∠DBC=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,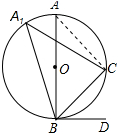
∴∠A+∠ABC=90°,
∴∠DBC=∠A=30°;
(2)连接AC,如图所示:
由(1)得:∠DBC=∠A,
又∵∠A=∠A1,
∴∠DBC=∠BA1C=40°;
(3)由(2)得:∠DBC=∠BA2C=α;
点评 本题考查了圆周角定理、弦切角定理;熟练掌握圆周角定理是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若x,y为实数,且|x+1|+$\sqrt{y-1}$=0,则xy的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
5.关于x的一元二次方程ax2+bx+c=0(a≠0)的两根如果互为倒数,那么( )
| A. | a=b | B. | b=c | C. | a=c | D. | a=b=c |
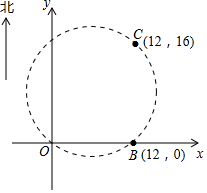 在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是“利剑-2016”中国多军种军事演习区,如图所示.
在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是“利剑-2016”中国多军种军事演习区,如图所示.
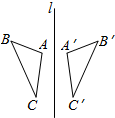 如图,△ABC与△A′B′C′关于直线l对称,且∠A=98°,∠C′=42°,则∠B的度数为40°.
如图,△ABC与△A′B′C′关于直线l对称,且∠A=98°,∠C′=42°,则∠B的度数为40°. (1)解方程:x2-2x=2x+1
(1)解方程:x2-2x=2x+1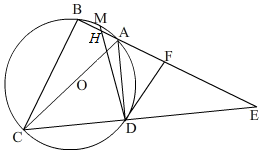 如图,⊙O是四边形ABCD的外接圆,AC是直径,分别延长AB、CD相交于点E,AC=AE,过点D作DF∥BC于点F.
如图,⊙O是四边形ABCD的外接圆,AC是直径,分别延长AB、CD相交于点E,AC=AE,过点D作DF∥BC于点F.