题目内容
1. (1)解方程:x2-2x=2x+1
(1)解方程:x2-2x=2x+1(2)如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.
分析 (1)利用配方法或公式法直接解方程即可;
(2)设AB为xm,则BC为(50-2x)m,根据题意可得等量关系:矩形的长×宽=300,根据等量关系列出方程,再解即可.
解答 解:
(1)∵x2-4x=1,
∴(x-2)2=5,
∴x1=2+$\sqrt{5}$;x2=2-$\sqrt{5}$;
(2)设AB为xm,则BC为(50-2x)m,
根据题意得方程:x(50-2x)=300,
2x2-50x+300=0,
解得;x1=10,x2=15,
当x1=10时50-2x=30>25(不合题意,舍去),
当x2=15时50-2x=20<25(符合题意).
答:当砌墙宽为15米,长为20米时,花园面积为300平方米.
点评 (1)此题考查了解一元二次方程的方法,熟记解方程的各种方法是解题的关键.
(2)此题主要考查了一元二次方程的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程.

练习册系列答案
相关题目
11.若x2+mx+1是完全平方式,则m=( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±4 |
6.已知直线y=kx+3经过点A(-1,2)且与x轴交于点B,点B的坐标是( )
| A. | (-3,0) | B. | (0,3) | C. | (3,0) | D. | (0,-3) |
11.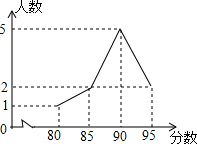 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )
 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )| A. | 88 | B. | 89 | C. | 90 | D. | 91 |
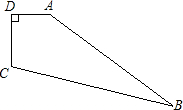 如图,在四边形ABCD中,∠D=90°,AD=3,DC=4,AB=12,BC=13.求四边形ABCD的面积.
如图,在四边形ABCD中,∠D=90°,AD=3,DC=4,AB=12,BC=13.求四边形ABCD的面积.