在一列数:a1.a2.a3.-.an中.a1=3.a2=7.从第三个数开始.每一个数都等于它前两个数之积的个位数字.则这一列数中的第2017个数是( )A．1B．3C．7D．9 题目和参考答案——青夏教育精英家教网—

题目内容

9．在一列数：a₁，a₂，a₃，…，a_n中，a₁=3，a₂=7，从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这一列数中的第2017个数是（　　）

A．

B．

C．

D．

分析本题可分别求出n=3、4、5…时的情况，观察它是否具有周期性，再把2017代入求解即可．

解答解：依题意得：a₁=3，a₂=7，a₃=1，a₄=7，a₅=7，a₆=9，a₇=3，a₈=7；
周期为6；
2017÷6=336…1，
所以a₂₀₁₇=a₁=3．
故选B．

点评本题考查了找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．而具有周期性的题目，找出周期是解题的关键．

练习册系列答案

相关题目

19．

如图表示下列四个不等式组中其中一个的解集，这个不等式组是（　　）

A．

$\left\{\begin{array}{l}{x≥2}\\{x＞-3}\end{array}\right.$

B．

$\left\{\begin{array}{l}{x≤2}\\{x＜-3}\end{array}\right.$

C．

$\left\{\begin{array}{l}{x≥2}\\{x＜-3}\end{array}\right.$

D．

$\left\{\begin{array}{l}{x≤2}\\{x＞-3}\end{array}\right.$

20．

如图，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4：3：5，则∠D的度数是120°．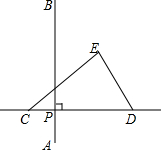

17．

如图，在平面内，线段AB=6，P为线段AB上的动点，三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P，且满足PC=PA．若点P沿AB方向从点A运动到点B，则点E运动的路径长为6$\sqrt{2}$．

a⁴•a

a³+a³

a⁴÷a

14．车辆经过润扬大桥收费站时，4个收费通道 A、B、C、D中，可随机选择其中的一个通过．
（1）一辆车经过此收费站时，选择 A通道通过的概率是$\frac{1}{4}$；
（2）求两辆车经过此收费站时，选择不同通道通过的概率．

1．

解不等式组：$\left\{{\begin{array}{l}{-2x＜6}\\{3（{x-2}）≤x-4}\end{array}}\right.$，并把解集在数轴上表示出来．

5．

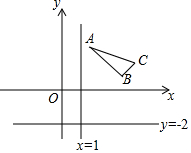如图，△ABC的顶点分别为A（2，3），B（4，1），C（5，2），分别作出△ABC关于直线x=1对称的图形△A₁B₁C₁和关于直线y=-2对称的图形△A₂B₂C₂．

6．

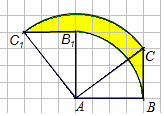如图，正方形网格中，△ABC为格点三角形（顶点都是格点），将△ABC绕点A按逆时针方向旋转90°得到△AB₁C₁，若网格小正方形的边长为1cm，则线段BC所扫过的图形（阴影部分）的面积为$\frac{9π}{4}$（结果保留π）．

试题分类