题目内容
6．
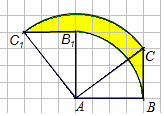如图，正方形网格中，△ABC为格点三角形（顶点都是格点），将△ABC绕点A按逆时针方向旋转90°得到△AB1C1，若网格小正方形的边长为1cm，则线段BC所扫过的图形（阴影部分）的面积为$\frac{9π}{4}$（结果保留π）．
分析 如图，BC扫过的部分通过割补，是一个$\frac{1}{4}$环形，由于△ABC是直角三角形，两直角边分别是3个格和5个格，由勾股定理得到斜边AC是5个格，环形的外圆半径是5，内圆半径是4，根据扇形面积公式即可得到结论．
解答 解：根据分析得到段BC所扫过的图形的面积为：$\frac{90•π•{5}^{2}}{360}$-$\frac{90•π•{4}^{2}}{360}$=$\frac{π}{4}$（52-42）=$\frac{9π}{4}$，
故答案为：$\frac{9π}{4}$．
点评 本题主要考查了图形的旋转，扇形的面积公式，勾股定理，能够通过割补知道BC扫过的部是一个$\frac{1}{4}$环形是解决问题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
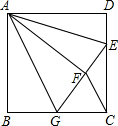如图，正方形ABCD中，AB=3，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF．下列结论：①点G是BC中点；②FG=FC；③与∠AGB相等的角有5个；④S△FGC=$\frac{9}{10}$．其中正确的有①④．
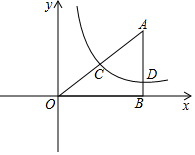如图，Rt△ABO在直角坐标系中，AB⊥x轴于点B，AO=10，sin∠AOB=$\frac{3}{5}$．
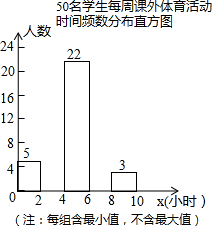为了解学生每周课外体育活动时间的情况，某学校随机调查了其中的50名学生，对这50名学生每周课外体育活动时间x（单位：小时）进行了统计．根据所得数据绘制了一幅不完整的统计图，并知道每周课外体育活动时间在6≤x＜8小时的学生人数占24%，根据以上信息及统计图解答下列问题：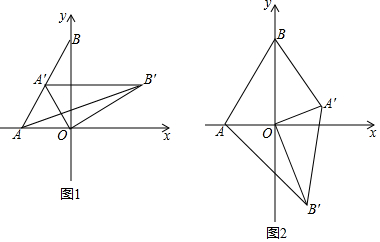
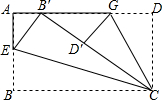如图，将一张矩形纸片ABCD的边BC斜着向AD边对折，使点B落在AD上，记为B′，折痕为CE；再将CD边斜向下对折，使点D落在B′C边上，记为D′，折痕为CG，B′D′=2，BE=$\frac{1}{3}$BC．则矩形纸片ABCD的面积为15．