题目内容
12.已知线段AB=4,延长AB到C,使AC=3AB,M为AC的中点,判断线段AB是不是线段BM和BC的比例中项,并说明理由.分析 根据已知条件求得AC=3×4=12,BC=8,由M为AC的中点,得到AM=$\frac{1}{2}$AC=6,进一步得到BM=AM-AB=2,由于AB2=42=16,BM•BC=2×8=16,于是得到AB2=BM•BC,即可得到结论.
解答 解:线段AB是线段BM和BC的比例中项,
理由:∵AB=4,AC=3AB,
∴AC=3×4=12,BC=8,
∵M为AC的中点,
∴AM=$\frac{1}{2}$AC=6,
∴BM=AM-AB=2,
∵AB2=42=16,BM•BC=2×8=16,
∴AB2=BM•BC,
∴$\frac{AB}{BM}=\frac{BC}{AB}$,
∴线段AB是线段BM和BC的比例中项.
点评 本题考查了线段上两点间距离,比例线段,解题的关键是理解比例中项的含义.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
17.为估计某一池塘中鱼的总数目,小英将100尾做了标记的鱼投入池塘中,几天后,随机捕捞,每次捕捞后做好记录,然后将鱼放回,如此进行20次,记录数据如下.
(1)估计该池塘原有多少尾鱼,你认为该估计准确吗?说明理由.
(2)你能否另外设计一个方案估计池塘的鱼数?
| 总条数 | 50 | 45 | 60 | 48 | 10 | 30 | 42 | 38 | 15 | 10 |
| 标记数 | 2 | 1 | 3 | 2 | 0 | 1 | 1 | 2 | 0 | 1 |
| 总条数 | 53 | 36 | 27 | 34 | 43 | 26 | 18 | 22 | 25 | 47 |
| 标记数 | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 |
(2)你能否另外设计一个方案估计池塘的鱼数?
 如图,已知线段AB,在线段AB上求作点C,使得AC:BC=2:1.(保留作图痕迹).
如图,已知线段AB,在线段AB上求作点C,使得AC:BC=2:1.(保留作图痕迹).
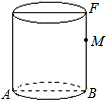 如图,已知圆柱体底面直径AB为2cm,高为4cm
如图,已知圆柱体底面直径AB为2cm,高为4cm