题目内容
17．
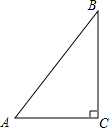如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，则cosA的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{3}$ |
分析 根据勾股定理，可得AB的长，根据余弦函数是邻边比斜边，可得答案．
解答 解：由勾股定理，得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5，
cosA=$\frac{AC}{AB}$=$\frac{3}{5}$，
故选：A．
点评 本题考查了锐角三角函数的定义，利用勾股定理得出AB的长是解题关键，又利用了余弦函数是邻边比斜边．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
7．平面直角坐标系，第四象限内一点P到x轴的距离为2，到y轴的距离为5，那么点P坐标是（ ）
| A． | （2，-5） | B． | （-5，2） | C． | （-2，5） | D． | （5，-2） |
5．下列运算正确的是（ ）
| A． | -（-a+b）=a+b | B． | 3a3-3a2=a | C． | （x6）2=x8 | D． | 1÷（$\frac{2}{3}$）-1=$\frac{2}{3}$ |
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：①b2-4ac＞0②abc＜0③2a+b＜0④m＞2其中，正确的是结论的个数是（ ）
2．下列运算正确的是（ ）
| A． | 2a•5b=10ab | B． | （2x2）3=2x5 | C． | 3+$\sqrt{2}$=3$\sqrt{2}$ | D． | $\sqrt{6}$÷$\sqrt{3}$=2 |
如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（-$\frac{9}{2}$，3 ），AB=2，AD=3．