题目内容
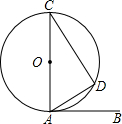如图，AB与⊙O相切于点A，AC为⊙O的直径，点D在圆上，且满足∠BAD=40°，则∠ACD的大小是（ ）| A、50° | B、45° |
| C、40° | D、42° |
考点：切线的性质
专题：
分析：根据切线的性质即可得到∠CAB=90°，从而求得∠CAD的度数，然后根据直径所对的圆周角是直角，可证明△ACD是直角三角形，根据直角三角形的性质求解．
解答：解：∵AB与⊙O相切于点A，
∴AC⊥AB，则∠CAB=90°，
∴∠CAD=90°-40°=50°，
又∵AC是⊙O的直径，
∴∠ADC=90°，
∴∠ACD=90°-∠CAD=90°-50°=40°．
故选C．
∴AC⊥AB，则∠CAB=90°，
∴∠CAD=90°-40°=50°，
又∵AC是⊙O的直径，
∴∠ADC=90°，
∴∠ACD=90°-∠CAD=90°-50°=40°．
故选C．
点评：本题考查了切线的性质以及圆周角定理，注意已知切线时要想到切线垂直于过切点的半径．
练习册系列答案
口算题天天练系列答案
相关题目
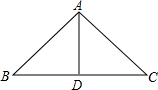如图，在△ABC中，AB=AC，∠BAC=90°，AD⊥BC，则下列结论不正确的是（ ）| A、∠BAD=45° | ||
| B、△ABD≌△ACD | ||
C、AD=
| ||
D、AD=
|