题目内容
6.如图,每个椭圆表示一个数集,请在每个椭圆内填上6个数,其中三个写在重叠部分,
分析 根据负数与整数集合重叠部分为负整数,列举出几个即可;根据正数与分数集合重叠部分为正分数,列举出几个即可.
解答 解:如图所示:
点评 此题考查了有理数,熟练掌握整数,分数与正、负数的定义是解本题的关键.

练习册系列答案
相关题目
15.某公司购进某种水果的成本为20元/千克,经过市场调研发现,这种水果在未来48天的销售价格p(元/千克)与时间t(天)之间的函数关系式为
p=$\left\{\begin{array}{l}{\frac{1}{4}t+30(1≤t≤24,t为整数)}\\{-\frac{1}{2}t+48(25≤t≤48,t为整数)}\end{array}\right.$,且其日销售量y(千克)与时间t(天)的关系如下表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1千克水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
p=$\left\{\begin{array}{l}{\frac{1}{4}t+30(1≤t≤24,t为整数)}\\{-\frac{1}{2}t+48(25≤t≤48,t为整数)}\end{array}\right.$,且其日销售量y(千克)与时间t(天)的关系如下表:
| 时间t/天 | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y/千克 | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1千克水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.

 已知,如图AB=AE,∠B=∠E,BC=ED,AF平分∠BAE,求证:AF⊥CD.
已知,如图AB=AE,∠B=∠E,BC=ED,AF平分∠BAE,求证:AF⊥CD. 如图,将一块长方形纸条折成如图的形状,若已知∠1=110°,则∠2=55°.
如图,将一块长方形纸条折成如图的形状,若已知∠1=110°,则∠2=55°.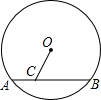 如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是$\sqrt{13}$.
如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是$\sqrt{13}$. 如图,AB,CD,EF交于点O,∠1=20°,∠2=60°,求∠BOC的度数.
如图,AB,CD,EF交于点O,∠1=20°,∠2=60°,求∠BOC的度数.