题目内容
14. 如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )
如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )| A. | 55° | B. | 70° | C. | 110° | D. | 140° |
分析 连接OA、OB,根据切线的性质定理,结合四边形AOBP的内角和为360°,即可推出∠AOB的度数,然后根据圆周角定理,即可推出∠C的度数.
解答 解:连接OA、OB, ∵直线PA、PB分别与⊙O相切于点A、B,
∵直线PA、PB分别与⊙O相切于点A、B,
∴OA⊥PA,OB⊥PB,
∵∠P=70°,
∴∠AOB=110°,
∵C是⊙O上一点,
∴∠ACB=55°.
故选A.
点评 本题主要考查切线的性质、四边形的内角和、圆周角定理,关键在于熟练运用切线的性质,通过作辅助线构建四边形,最后通过圆周角定理即可推出结果.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5. 如图,点A和B表示的数分别为a和b,下列式子中,不正确的是( )
如图,点A和B表示的数分别为a和b,下列式子中,不正确的是( )
 如图,点A和B表示的数分别为a和b,下列式子中,不正确的是( )
如图,点A和B表示的数分别为a和b,下列式子中,不正确的是( )| A. | a>-b | B. | ab<0 | C. | a-b>0 | D. | a+b>0 |
9.抛物线y=(x-1)2-3的顶点坐标是( )
| A. | (-1,-3) | B. | (-1,3) | C. | (1,-3) | D. | (1,3) |
19.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则应满足的条件是( )
| A. | x≠1 | B. | x=-1 | C. | x=1 | D. | x=±1 |
6.将抛物线y=2x2平移得到抛物线y=2(x-2)2+3,下列平移正确的是( )
| A. | 先向左平移2个单位,再向上平移3个单位 | |
| B. | 先向左平移2个单位,再向下平移3个单位 | |
| C. | 先向右平移2个单位,再向下平移3个单位 | |
| D. | 先向右平移2个单位,再向上平移3个单位 |
4.若-2am+4b4与5a2bn+1可以合并成一项,则mn的值是( )
| A. | -6 | B. | 8 | C. | -8 | D. | 9 |
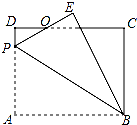 如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为2.4.
如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为2.4.