题目内容
2.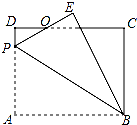 如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为2.4.
如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为2.4.
分析 由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=4,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=3-x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
解答 解:如图所示: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=3,CD=AB=4,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=4,
在△ODP和△OEG中,
$\left\{\begin{array}{l}{∠D=∠E}&{\;}\\{OD=OE}&{\;}\\{∠DOP=∠EOG}&{\;}\end{array}\right.$,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=3-x,DG=x,
∴CG=4-x,BG=4-(3-x)=1+x,
根据勾股定理得:BC2+CG2=BG2,
即32+(4-x)2=(x+1)2,
解得:x=2.4,
∴AP=2.4;
故答案为:2.4.
点评 本题考查了矩形的性质、折叠的性质、全等三角形的判定与性质、勾股定理;熟练掌握翻折变换和矩形的性质,由勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
13.已知一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,点A在此函数图象上,则点A坐标不可能是( )
| A. | (2,3) | B. | (-3,-1) | C. | (3,-1) | D. | (-1,1) |
10.甲,乙,丙三地的海拔高度为20米,-15米,-10米,那么最高地方是( )
| A. | 20米 | B. | -10米 | C. | -15米 | D. | 15米 |
17.下列代数式书写正确的是( )
| A. | a48 | B. | x÷y | C. | a(x+y) | D. | a×b×c |
7.如果多项式y2-2my+1是完全平方式,那么m的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 无法确定 |
14. 如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )
如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )
 如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )
如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )| A. | 55° | B. | 70° | C. | 110° | D. | 140° |
11. 如图中,到原点距离相等的两个点是( )
如图中,到原点距离相等的两个点是( )
 如图中,到原点距离相等的两个点是( )
如图中,到原点距离相等的两个点是( )| A. | 点M与点Q | B. | 点N与点P | C. | 点M与点P | D. | 点N与点Q |
12.一组数据a、b、c、d、e、f、g的平均数是m,方差是n,则另一组数据2a-3、2b-3、2c-3、2d-3、2e-3、2f-3、2g-3的平均数和方差分别是( )
| A. | 2m、2n-3 | B. | 2m-3、n | C. | m-3、2n | D. | 2m-3、4n |
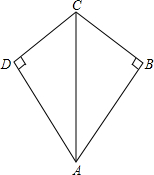 如图,四边形ABCD中,CB=CD,∠B=∠D=90°,∠BAD=60°,则∠ACB的度数为60°.
如图,四边形ABCD中,CB=CD,∠B=∠D=90°,∠BAD=60°,则∠ACB的度数为60°.