题目内容
19.线段AB,BC均在直线l上,若AB=12,AC=4,M与N分别是AB,AC的中点,则MN的长为4cm或8cm.分析 画出图形,得出两种情况,(1)点C在线段AB上,(2)点C在线段BA的延长线上,分别求出AN和AM长,即可得出答案.
解答 解:(1)点C在线段AB上,如: ,
,
∵点M是线段AB的中点,点N是线段AC的中点,
AM=$\frac{1}{2}$AB=6cm,AN=$\frac{1}{2}$AC=2cm,
MN=AM-AN=6cm-2cm=4cm;
(2)点C在线段BA的延长线上,如:
∵点M是线段AB的中点,点N是线段AC的中点,
AM=$\frac{1}{2}$AB=6cm,AN=$\frac{1}{2}$AC=2cm,
MN=AM+AN=6cm+2cm=8cm;
即MN=4cm或8cm,
故答案为:4cm或8cm.
点评 本题考查了求两点之间的距离的应用,能求出符合条件的所有情况是解此题的关键.

练习册系列答案
相关题目
10.如果$\frac{a}{b}$=$\frac{c}{d}$,那么下列四个选项中,不正确的是( )
| A. | $\frac{c}{a}$=$\frac{d}{b}$ | B. | ad=bc | C. | a:d=c:b | D. | a:b=c:d |
4.下列说法中,正确的是( )
| A. | 一个有理数,如果它不是正数,那么它一定是负数 | |
| B. | a的倒数是$\frac{1}{a}$ | |
| C. | 若盈利26元记作+26元,则亏损68元记作-68元 | |
| D. | 绝对值等于它本身的数是l |
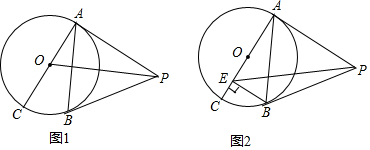 已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.
已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.