题目内容
4.某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在50≤x≤120时,具有一次函数的关系,如表所示.| x | 50 | 80 | 100 | 120 |
| y | 40 | 34 | 30 | 26 |
(2)如果修建70天,那么平均每天的修建费是多少?
分析 (1)设y与x之间的函数关系式为y=kx+b,运用待定系数法就可以求出y与x之间的函数关系式;
(2)把x=70代入(1)中的函数解析式可得y的值.
解答 解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),由题意,得
$\left\{\begin{array}{l}{40=50k+b}\\{38=60k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{5}}\\{b=50}\end{array}\right.$,
∴y与x之间的函数关系式为:y=-$\frac{1}{5}$x+50(30≤x≤120);
(2)当x=70时,y=-$\frac{1}{5}$×70+50=36,
答:平均每天的修建费是36万元.
点评 本题考查了运用待定系数法求函数的解析式的运用,关键是掌握待定系数法求一次函数解析式的方法.

练习册系列答案
相关题目
19.已知两个一次函数y1,y2的图象相互平行,它们的部分自变量与相应的函数值如表:
则m的值是( )
| x | m | 0 | 2 |
| y1 | 4 | 3 | t |
| y2 | 6 | n | -1 |
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | 5 |
9.下列整式中,属于多项式的是( )
| A. | a-2b | B. | -2ab | C. | -2 | D. | a |
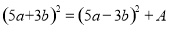 ,则A=( )
,则A=( ) 菱形ABCD的边AB为5,对角线AC为8,则菱形ABCD的面积为24.
菱形ABCD的边AB为5,对角线AC为8,则菱形ABCD的面积为24.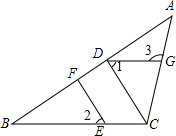 如图,在△ABC中,DG∥BC,∠1=∠2.
如图,在△ABC中,DG∥BC,∠1=∠2.