题目内容
8.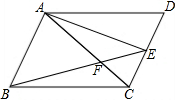 如图,已知四边形ABCD中,AD∥BC,∠ABC=∠ACD=∠D,AE平分∠CAD,下列说法:①AB∥CD;②AE⊥CD;③S△AEF=S△BCF;④∠AFB=∠BAD-∠ABE,其中正确的结论有( )
如图,已知四边形ABCD中,AD∥BC,∠ABC=∠ACD=∠D,AE平分∠CAD,下列说法:①AB∥CD;②AE⊥CD;③S△AEF=S△BCF;④∠AFB=∠BAD-∠ABE,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据∠ABC=∠D,AD∥BC得出平行四边形ABCD,即可推出AB∥CD;根据等腰三角形性质求出AE⊥CD,然后根据平行线的性质即可推出AE⊥AB;根据等底等高的三角形面积相等即可推出S△ABE=S△ABC,可得S△AEF=S△BCF;根据∠CFE+∠BEC+∠ACD=180°,∠BAD+∠D=180°,∠D=∠ACD,即可推出∠CFE+∠BEC=∠BAD;
解答 解:∵AD∥BC,
∴∠BAD+∠ABC=180°,∠D+∠BCD=180°,
∵∠ABC=∠D,
∴∠BAD=∠BCD,
∵∠ABC=∠D,
∴四边形ABCD是平行四边形,
∴AB∥CD,故①正确,
∵∠D=∠ACD,AE平分∠CAD,
∴AE⊥CD,故②正确,
∵S△ABE=S△ABC=$\frac{1}{2}$S平行四边形ABCD,
∴S△AEF=S△BCF,故③正确,
∵AB∥CD,
∴∠ABE=∠BEC,
∵∠AFB=∠EFC,
∴∠AFB+∠ABE=∠CFE+∠BEC,
∵∠CFE+∠BEC+∠ACD=180°,∠BAD+∠D=180°,∠D=∠ACD,
∴∠CFE+∠BEC=∠BAD,即∠AFB=∠BAD-∠ABE,故④正确,
∴①②③④正确,
故选D.
点评 本题考查了平行四边形的性质和判定,平行线性质,等腰三角形的性质,三角形的面积的应用,关键是推出AB∥CD.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
19.方程2x+y=6的正整数解有( )组.
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 无数组 |
20.若(x-y+3)2+|2x+y|=0,则xy的值为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
 已知二次函数y=-$\frac{1}{2}$x2-x+$\frac{3}{2}$.
已知二次函数y=-$\frac{1}{2}$x2-x+$\frac{3}{2}$.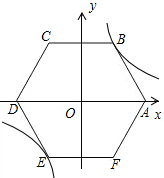 如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=$\frac{9\sqrt{3}}{x}$位于第一象限的图象上,则正六边形ABCDEF的边长为6.
如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=$\frac{9\sqrt{3}}{x}$位于第一象限的图象上,则正六边形ABCDEF的边长为6.