题目内容
14.计算下列各式,使得结果的分母中不含有二次根式:(1)$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$;
(2)$\frac{1}{\sqrt{32}}$=$\frac{\sqrt{2}}{8}$;
(3)$\frac{\sqrt{2}}{2\sqrt{3}}$=$\frac{\sqrt{6}}{6}$;
(4)$\frac{x}{\sqrt{5y}}$=$\frac{x\sqrt{5y}}{5y}$.
分析 (1)把分式的分子分母同时乘以$\sqrt{5}$即可;
(2)把分母化为4$\sqrt{2}$的形式,再把分式的分子与分母同时乘以$\sqrt{2}$即可;
(3)把分式的分子分母同时乘以即可;
(4)把分式的分子分母同时乘以$\sqrt{5y}$即可.
解答 解:(1)原式=$\frac{\sqrt{5}}{\sqrt{5}•\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$;
(2)原式=$\frac{1}{4\sqrt{2}}$=$\frac{\sqrt{2}}{4\sqrt{2}•\sqrt{2}}$=$\frac{\sqrt{2}}{8}$.
故答案为:$\frac{\sqrt{2}}{8}$;
(3)原式=$\frac{\sqrt{2}•\sqrt{3}}{2\sqrt{3}•\sqrt{3}}$=$\frac{\sqrt{6}}{6}$.
故答案为:$\frac{\sqrt{6}}{6}$;
(4)原式=$\frac{x\sqrt{5y}}{\sqrt{5y}•\sqrt{5y}}$=$\frac{x\sqrt{5y}}{5y}$.
故答案为:$\frac{x\sqrt{5y}}{5y}$.
点评 本题考查的是分母有理化,熟知分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式是解答此题的关键.

练习册系列答案
相关题目
4. 如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
 如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )
如图,E是△ABC的内心,若∠BEC=130°,则∠A的度数是( )| A. | 60° | B. | 80° | C. | 50° | D. | 75° |
2. 如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是( )
如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是( )
 如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是( )
如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是( )| A. | 3 | B. | 2.5 | C. | 2 | D. | 1.5 |
9.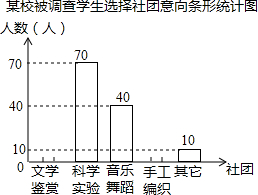 为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
某校被调查学生选择社团意向统计表
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的人数.
 为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):某校被调查学生选择社团意向统计表
| 选择意向 | 所占百分比 |
| 文学鉴赏 | a |
| 科学实验 | 35% |
| 音乐舞蹈 | b |
| 手工编织 | 10% |
| 其他 | c |
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的人数.
6.如图,下列图形是一组按照某种规律摆放而成的图案,则图⑧中圆点的个数是( )


| A. | 64 | B. | 65 | C. | 66 | D. | 67 |
 如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.
如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.