题目内容
1.一个不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是蓝球的概率为$\frac{1}{4}$.(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用树状图法或列表法,求两次摸出都是红球的概率;
(3)现规定:摸到红球得3分,摸到黄球得2分,摸到蓝球得1分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机再摸一次,求乙同学一次摸球所得分数之和不低于6分的概率.
分析 (1)设口袋中黄球的个数为x个,则根据概率公式得到$\frac{1}{2+1+x}$=$\frac{1}{4}$,然后解方程即可;
(2)画树状图展示所有12种等可能的结果数,再找出两次摸出都是红球的结果数,然后根据概率公式求解;
(3)画树状图展示所有16种等可能的结果数,再找出乙同学一次摸球所得分数之和不低于6分的结果数,然后根据概率公式求解.
解答 解:(1)设口袋中黄球的个数为x个,
根据题意得$\frac{1}{2+1+x}$=$\frac{1}{4}$,解得x=1,
所以口袋中有1个黄球;
(2)画树状图为:
共有12种等可能的结果数,其中两次摸出都是红球的结果数为2,
所以两次摸出都是红球的概率=$\frac{2}{12}$=$\frac{1}{6}$;
(3)画树状图为:
共有16种等可能的结果数,其中乙同学一次摸球所得分数之和不低于6分的结果数为12,
所以乙同学一次摸球所得分数之和不低于6分的概率=$\frac{12}{16}$=$\frac{3}{4}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
16.绿豆加工成绿豆芽后,重量比原来增加了7倍,要得到绿豆芽30千克,需要绿豆多少千克?若设需要绿豆x千克,则可以列出方程( )
| A. | 7x=30 | B. | x+7x=30 | C. | x+30=7x | D. | x+7=30 |
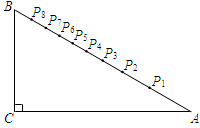 如图,小明设计了一个“简易量角器”:在△ABC中,∠C=90°,∠A=30°,CA=24cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
如图,小明设计了一个“简易量角器”:在△ABC中,∠C=90°,∠A=30°,CA=24cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°. 如图,AC与BD相交于点O,BO=2OC,AO=2OD.求证:△AOB∽△DOC.
如图,AC与BD相交于点O,BO=2OC,AO=2OD.求证:△AOB∽△DOC. 如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE,证明:△ABC∽△CDE.
如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE,证明:△ABC∽△CDE. 如图,已知在△ABC中,BC=10cm,AB的垂直平分线EF交BC与点F,AC的垂直平分线MN交BC于点N,则△AFN的周长为10cm.
如图,已知在△ABC中,BC=10cm,AB的垂直平分线EF交BC与点F,AC的垂直平分线MN交BC于点N,则△AFN的周长为10cm.